Машинное обучение
Введение в машинное обучение
Определение машинного обучения
Машинное обучение (МО) - это подраздел искусственного интеллекта, который фокусируется на разработке систем, способных обучаться на основе данных. Основная идея машинного обучения заключается в создании алгоритмов и моделей, которые могут адаптироваться к данным, обнаруживать паттерны, принимать решения и улучшать свою производительность с опытом, вместо явного программирования для выполнения конкретной задачи.
Основные элементы машинного обучения
Данные: Машинное обучение требует доступа к данным, на которых модель может обучиться. Эти данные могут быть размеченными (содержат правильные ответы) или неразмеченными.
Модели: Это математические структуры, построенные на основе данных, которые могут делать предсказания или принимать решения без явного программирования.
Обучение: Процесс обучения модели на данных, который включает в себя настройку параметров модели таким образом, чтобы она могла лучше соответствовать данным и делать более точные предсказания.
Прогнозирование и принятие решений: После завершения процесса обучения модель может использоваться для прогнозирования результатов новых данных или принятия решений на основе полученного опыта.
Примеры задач машинного обучения включают классификацию (разделение данных на категории), регрессию (прогнозирование числовых значений), кластеризацию (группировка данных на основе их схожести) и многое другое. Машинное обучение применяется в различных областях, включая медицину, финансы, технологии, исследования и многое другое.
Различие между программированием и машинным обучением.
Явное программирование
Программирование: Традиционное программирование включает создание явных инструкций и правил для решения конкретной задачи. Программист определяет шаги, которые система должна выполнить, чтобы достичь желаемого результата.
Пример: Если задача - определить, является ли число четным или нечетным, программист напишет явные условия проверки деления на 2.
Машинное обучение
Программирование: В случае машинного обучения, вместо того чтобы явно задавать шаги, программа обучается на основе данных. Модель адаптируется к обучающим данным, извлекая паттерны и взаимосвязи, что позволяет ей делать предсказания для новых данных.
Пример: В задаче классификации изображений, модель может обучиться распознавать образы кошек и собак, а затем использовать этот опыт для классификации новых изображений.
Ключевые различия
В явном программировании правила задаются человеком, в машинном обучении модель сама извлекает правила из данных.
Машинное обучение предоставляет более гибкий подход к решению задач, особенно в условиях сложных и изменяющихся данных.
Роль машинного обучения в решении сложных задач
- Обработка больших объемов данных:
- Машинное обучение эффективно обрабатывает огромные объемы данных, извлекая из них сложные закономерности и паттерны, которые могут быть трудны для восприятия человеком.
- Комплексные взаимосвязи:
- В сложных задачах, где есть множество взаимосвязанных факторов, машинное обучение может автоматически выявлять нелинейные зависимости и взаимосвязи, что часто бывает сложно для формализации вручную.
- Прогнозирование:
- Машинное обучение позволяет строить модели для прогнозирования будущих событий на основе анализа исторических данных. Это применяется в финансах, метеорологии, здравоохранении и других областях.
- Автоматизация рутинных задач:
- В сфере бизнеса и производства машинное обучение может автоматизировать рутинные задачи, освобождая время человека для более творческой и стратегической работы.
- Поиск скрытых шаблонов:
- Модели машинного обучения способны обнаруживать скрытые шаблоны и тенденции в данных, которые могли бы остаться незамеченными человеком.
- Персонализация:
- В маркетинге и интернет-сервисах машинное обучение позволяет создавать персонализированные рекомендации и предложения, учитывая уникальные предпочтения и потребности каждого пользователя.
Преимущества автоматизации процессов и принятия решений
- Эффективность и ускорение процессов:
- Автоматизация процессов с использованием машинного обучения позволяет ускорить выполнение задач и снизить время, требуемое для их завершения.
- Уменьшение ошибок:
- Автоматизированные системы на основе машинного обучения способны снижать вероятность ошибок, поскольку они могут адаптироваться к новым данным и обучаться на опыте.
- Адаптивность к изменениям:
- Модели машинного обучения могут быстро адаптироваться к изменяющимся условиям и требованиям, что особенно важно в средах с быстро меняющейся динамикой.
- Высокая точность прогнозов:
- Автоматизированные системы, обученные на больших объемах данных, могут обеспечить более точные прогнозы и предсказания, что важно для принятия стратегических решений.
- Экономия ресурсов:
- Автоматизация процессов позволяет оптимизировать использование ресурсов, таких как время и энергия, что приводит к повышению эффективности бизнес-процессов.
Основные концепции
Понятие обучения на примерах и обучения на данных
- Обучение на примерах:
- Это форма обучения в машинном обучении, при которой модель обучается на основе предоставленных ей примеров данных. Каждый пример состоит из входных данных и соответствующего правильного ответа (целевой переменной). Модель использует эти примеры для извлечения паттернов и закономерностей, которые позволяют ей делать предсказания на новых данных.
- Обучение на данных:
- Это более общее понятие, охватывающее не только обучение на примерах, но также обучение на данных в более широком смысле. В этом контексте обучение может включать в себя извлечение информации из данных, выделение признаков, снижение размерности и другие методы работы с информацией.
Роль моделей и алгоритмов в машинном обучении
- Модели в машинном обучении:
- Модель представляет собой абстракцию, которая используется для описания процесса, в основе которого лежат данные. В контексте машинного обучения модель - это математическое представление системы, которое может использоваться для прогнозирования, классификации, кластеризации и других задач.
- Роль моделей:
- Модель принимает на вход данные, обучается на них, извлекает закономерности и использует эти знания для выполнения конкретной задачи. Например, линейная регрессия представляет собой модель для предсказания числовых значений, а сверточные нейронные сети используются для обработки изображений.
- Алгоритмы в машинном обучении:
- Алгоритм - это набор шагов или инструкций, которые определяют, как модель обучается на данных или как выполняется конкретная задача. Например, алгоритм градиентного спуска используется для обучения весов модели в задачах регрессии и классификации.
- Роль алгоритмов:
- Алгоритмы в машинном обучении определяют, каким образом модель должна адаптироваться к данным. Они включают в себя методы оптимизации, функции потерь и другие техники, которые позволяют модели наилучшим образом приближаться к правильным ответам.
- Выбор моделей и алгоритмов:
- Выбор конкретной модели и алгоритма зависит от характера задачи, типа данных, доступности ресурсов и других факторов. Например, для изображений часто используют сверточные нейронные сети, а для задачи регрессии может быть выбрана линейная регрессия.
Типы машинного обучения
Надзорное обучение
Обучение с учителем и размеченные данные
- Обучение с учителем:
- Обучение с учителем — это тип машинного обучения, при котором модель обучается на основе размеченных данных, где каждый пример данных сопровождается правильным ответом (целевой переменной). Модель стремится извлечь закономерности из этого набора данных, чтобы способствовать правильным предсказаниям на новых, ранее не виденных данных.
- Размеченные данные:
- Размеченные данные — это данные, в которых для каждого примера известен правильный ответ. Например, в задаче классификации изображений кошек и собак каждому изображению присвоен ярлык (метка), указывающий, к какому классу оно относится.
Примеры задач
- Классификация:
- Определение категории объекта.
- Пример: Распознавание электронных писем как спама или неспама. Модель обучается на размеченных данных, где каждое письмо помечено как “спам” или “не спам”, и затем использует этот опыт для классификации новых писем.
- Распознавание рукописных цифр.
- Пример: Модель обучается на наборе изображений рукописных цифр с указанием соответствующей цифры. Затем она может классифицировать новые изображения цифр, которые не были включены в обучающий набор.
- Определение категории объекта.
- Регрессия:
- Прогнозирование числового значения.
- Пример: Предсказание стоимости недвижимости на основе характеристик, таких как площадь, количество комнат и местоположение. Модель обучается на размеченных данных, где каждому наблюдению соответствует фактическая цена, и затем предсказывает цену для новых наблюдений.
- Оценка вероятности заболевания.
- Пример: Модель обучается на медицинских данных с указанием наличия или отсутствия конкретного заболевания. Затем, на основе новых медицинских данных, модель может предсказывать вероятность заболевания у пациента.
- Прогнозирование числового значения.
В обоих случаях - классификации и регрессии, модели обучаются на основе размеченных данных с известными ответами, что позволяет им выявлять закономерности и делать предсказания для новых, ещё не виденных данных.
Безнадзорное обучение
Обучение без учителя и неразмеченные данные
- Обучение без учителя:
- Обучение без учителя — это подход в машинном обучении, при котором модель обучается на неразмеченных данных, то есть данных, где нет предварительно указанных правильных ответов. Задача модели заключается в извлечении структуры или паттернов из данных без явного руководства.
- Неразмеченные данные:
- Неразмеченные данные — это данные, в которых отсутствуют явные метки или целевые переменные. В отличие от обучения с учителем, где каждый пример сопровождается известным ответом, здесь модели приходится самой искать структуру в данных.
Примеры задач
- Кластеризация:
- Группировка данных на основе их схожести.
- Пример: Кластеризация клиентов интернет-магазина на основе их покупательского поведения. Модель обнаруживает группы клиентов с похожими предпочтениями, что может быть использовано для персонализации маркетинговых стратегий.
- Классификация изображений без явных меток.
- Пример: Модель, обученная на большом наборе изображений, где отсутствуют явные классы, может кластеризовать изображения по их визуальной схожести, выделяя группы изображений с похожими характеристиками.
- Группировка данных на основе их схожести.
- Снижение размерности:
- Уменьшение количества признаков, сохраняя важную информацию.
- Пример: Снижение размерности данных в задаче анализа текстов для поиска основных тем. Модель может сократить признаки (слова) таким образом, чтобы сохранить ключевые тематические особенности документов.
- Уменьшение размерности изображений для ускорения обработки.
- Пример: Модель снижения размерности изображений для упрощения их представления с минимальной потерей информации. Это может быть полезно, например, в случае обработки медицинских изображений.
- Уменьшение количества признаков, сохраняя важную информацию.
В задачах обучения без учителя, модели стремятся найти структуру, связь или группировку в данных без явных указаний о том, что искать. Кластеризация и снижение размерности являются примерами задач, где обучение без учителя может быть эффективно использовано для извлечения скрытых паттернов в неразмеченных данных.
Подкрепленное обучение
Агенты, среда и обратная связь в контексте машинного обучения
- Агент:
- Агент - это сущность, принимающая решения и действующая в некоторой среде. В машинном обучении агент обычно представляет собой модель или систему, способную принимать решения на основе опыта.
- Среда:
- Среда - это контекст, в котором действует агент. Среда включает в себя все факторы и условия, которые могут повлиять на агента и на его принимаемые решения.
- Обратная связь:
- Обратная связь представляет собой механизм, с помощью которого агент получает информацию о том, насколько успешными были его действия в данной среде. Обратная связь может быть положительной (поощряющей) или отрицательной (наказывающей), и она служит для коррекции будущих решений агента.
Примеры задач и применений
- Обучение с подкреплением:
- Определение лучших действий в заданной среде.
- Пример: Обучение агента-робота в среде производства для оптимизации его действий и максимизации производительности. Робот получает обратную связь в виде награды (например, успешное выполнение задачи) или штрафа (например, повреждение оборудования).
- Обучение игрового агента в видеоигре.
- Пример: Агент играет в компьютерную игру и получает обратную связь в зависимости от своих действий. Задача агента - максимизировать свой счет или достигнуть определенного уровня.
- Определение лучших действий в заданной среде.
- Системы рекомендаций:
- Предоставление персонализированных рекомендаций.
- Пример: Система рекомендаций в интернет-магазине. Агент анализирует предпочтения пользователя (среда) и предлагает ему товары на основе предыдущих покупок и предпочтений. Обратная связь - покупка или отклонение предложенных товаров.
- Предоставление персонализированных рекомендаций.
- Автономные транспортные средства:
- Принятие решений на дороге.
- Пример: Автономный автомобиль (агент) перемещается в городской среде, принимая решения о маневрах, учете дорожной обстановки и безопасности. Обратная связь может быть предоставлена через датчики, системы навигации и реакции других участников движения.
- Принятие решений на дороге.
- Финансовые торговые алгоритмы:
- Принятие решений о покупке/продаже акций.
- Пример: Торговый агент анализирует рыночные данные (среда) и принимает решения о покупке или продаже акций. Обратная связь предоставляется в виде прибыли или убытка от совершенных сделок.
- Принятие решений о покупке/продаже акций.
Агенты, среда и обратная связь широко используются в различных областях для создания систем, способных адаптироваться к изменяющимся условиям и принимать эффективные решения в различных сценариях.
Основные алгоритмы машинного обучения
Линейная регрессия
Описание модели:
Линейная регрессия — это метод в машинном обучении, используемый для моделирования отношений между зависимой переменной (выходом) и одной или несколькими независимыми переменными (признаками). Базовая идея линейной регрессии заключается в поиске линейной зависимости между признаками и целевой переменной.
Основные принципы
- Линейная модель:
- Модель линейной регрессии представляется уравнением прямой: \(y = b_0 + b_1 \cdot x_1 + b_2 \cdot x_2 + \ldots + b_n \cdot x_n\) где (y) — зависимая переменная, \(x_1, x_2, \ldots, x_n\) — независимые переменные, \(b_0\) — свободный член (пересечение с осью (y)), а \(b_1, b_2, \ldots, b_n\) — коэффициенты, которые определяют наклон прямой по каждой из осей.
- Минимизация ошибки:
- Цель линейной регрессии — минимизировать сумму квадратов разностей между фактическими значениями и предсказанными значениями. Это достигается путем подбора коэффициентов \(b_0, b_1, \ldots, b_n\) так, чтобы минимизировать функцию потерь.
- Обучение:
- Обучение модели включает в себя настройку коэффициентов \(b_0, b_1, \ldots, b_n\) на основе обучающих данных. Это может быть сделано различными методами, включая метод наименьших квадратов или градиентный спуск.
Примеры применения в реальных задачах
- Прогнозирование цен на недвижимость:
- Линейная регрессия может использоваться для прогнозирования стоимости недвижимости на основе различных факторов, таких как площадь жилья, количество комнат, удаленность от центра и другие.
- Экономический анализ:
- В экономике линейная регрессия может быть применена для анализа зависимости между различными экономическими переменными, такими как ВВП, инфляция, безработица и т.д.
- Маркетинговый анализ:
- В маркетинге линейная регрессия может использоваться для определения влияния различных маркетинговых стратегий на продажи продуктов.
- Медицинская статистика:
- В медицинских исследованиях линейная регрессия может быть применена для анализа влияния различных факторов на здоровье пациентов, например, на связь между уровнем физической активности и уровнем холестерина.
Линейная регрессия является простым и широко используемым методом, который остается актуальным во многих областях из-за своей интерпретируемости и эффективности в различных сценариях.
Метод k ближайших соседей (k-NN)
Принцип работы алгоритма
Метод k ближайших соседей (k-NN) — это простой и популярный алгоритм машинного обучения, используемый для задач классификации и регрессии. Принцип работы алгоритма основан на простой идее: объекты, близкие в пространстве признаков, имеют схожие характеристики.
- Классификация:
- Для классификации объекта алгоритм находит k ближайших соседей этого объекта в пространстве признаков. Класс объекта определяется на основе классов его ближайших соседей: объект относится к классу, который наиболее представлен среди k ближайших соседей.
- Регрессия:
- В случае регрессии, вместо классов, объектам присваиваются числовые значения. Например, значение объекта может быть усреднением значений его ближайших соседей.
- Выбор k:
- Параметр k представляет собой количество ближайших соседей, которые используются для принятия решения. Выбор значения k влияет на точность и стабильность модели: небольшие значения k могут привести к переобучению, в то время как большие значения k могут привести к упрощению модели.
- Метрика расстояния:
- Для определения “близости” объектов используется метрика расстояния, обычно евклидово расстояние. Однако, в зависимости от задачи, могут применяться и другие метрики.
Примеры использования для классификации
- Распознавание рукописных цифр:
- Задача: Классификация изображений рукописных цифр.
- Применение: Алгоритм k-NN может быть использован для определения, к какому классу (цифре) относится каждое изображение, основываясь на схожести с ближайшими соседями в пространстве пикселей.
- Системы рекомендаций в электронной коммерции:
- Задача: Рекомендация продуктов покупателям на основе их предпочтений и покупок других клиентов.
- Применение: k-NN может определить схожесть между потребителями, основываясь на их покупках, и рекомендовать товары, которые понравились их ближайшим соседям.
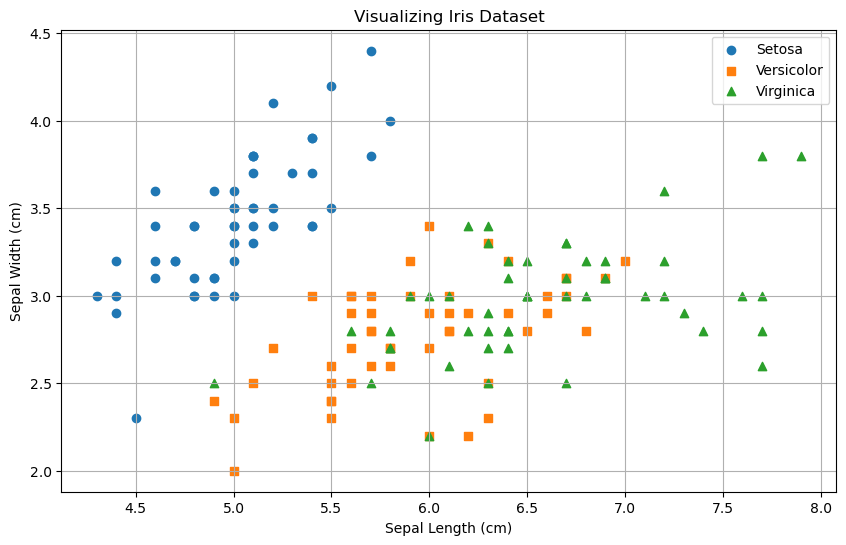
- Определение типа цветка по его характеристикам:
- Определение темы текста:
- Задача: Классификация текстов по их содержанию.
- Применение: k-NN может классифицировать тексты, опираясь на схожесть слов и структуры текста с ближайшими соседями из обучающего набора.
k-NN широко используется в реальных задачах, особенно там, где данные нелинейны и сложно выделить четкие закономерности.
Пример приложения на Python
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.metrics import accuracy_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
# # Генерация большего количества данных для обучения и предсказания
# X, y = np.random.rand(100, 2), np.random.choice([0, 1], size=100)
# # Разделение данных на тренировочный и тестовый наборы
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Пример данных
X_train = np.array([[1, 2],[1.5, 1.5], [2, 3], [3, 4],[4, 4], [4, 5]])
y_train = np.array([0, 0, 0, 1, 1, 1])
X_test = np.array([[2, 4],[1, 3]])
y_test = np.array([1, 1]) # Фактические метки для тестового набора
# Метод k-ближайших соседей
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
predictions = [self._predict(x) for x in X]
return np.array(predictions)
def _predict(self, x):
distances = euclidean_distances([x], self.X_train)
k_neighbors_indices = np.argsort(distances[0])[:self.k]
k_neighbor_labels = [self.y_train[i] for i in k_neighbors_indices]
most_common = np.bincount(k_neighbor_labels).argmax()
return most_common
# Инициализируем и обучаем модель k-NN
knn = KNN(k=5)
knn.fit(X_train, y_train)
# Делаем предсказания
predictions_train = knn.predict(X_train)
predictions_test = knn.predict(X_test)
print(predictions_test);
# Оцениваем точность, полноту и F1-меру модели на тренировочных и тестовых данных
acc_train = accuracy_score(y_train, predictions_train)
rec_train = recall_score(y_train, predictions_train)
f1_train = f1_score(y_train, predictions_train)
acc_test = accuracy_score(y_test, predictions_test)
rec_test = recall_score(y_test, predictions_test)
f1_test = f1_score(y_test, predictions_test)
print("Точность на тренировочных данных:", acc_train)
print("Полнота на тренировочных данных:", rec_train)
print("F1-мера на тренировочных данных:", f1_train)
print("\nТочность на тестовых данных:", acc_test)
print("Полнота на тестовых данных:", rec_test)
print("F1-мера на тестовых данных:", f1_test)Метод опорных векторов (Support Vector Machines, SVM)
Метод опорных векторов (Support Vector Machines, SVM) — это алгоритм машинного обучения, который используется как для задач классификации, так и для регрессии. Главная идея SVM заключается в том, чтобы найти оптимальную гиперплоскость, разделяющую объекты разных классов в пространстве признаков. Оптимальность означает максимальное расстояние (зазор) между этой гиперплоскостью и объектами обоих классов.
Основные концепции и термины, связанные с методом опорных векторов:
- Гиперплоскость (Hyperplane):
- В n-мерном пространстве гиперплоскость - это (n-1)-мерное подпространство. В случае SVM, гиперплоскость используется для разделения пространства признаков на два класса.
- Опорные векторы (Support Vectors):
- Это точки данных, которые лежат ближе всего к гиперплоскости и влияют на ее положение. Оптимальная гиперплоскость определяется именно этими опорными векторами.
- Зазор (Margin):
- Зазор - это расстояние между оптимальной гиперплоскостью и ближайшими к ней опорными векторами. Основная цель SVM - максимизировать этот зазор.
- Ядро (Kernel):
- Ядро в SVM - это функция, которая преобразует данные в более высокоразмерное пространство, делая их линейно разделимыми. Популярные ядра включают полиномиальные, радиальные базисные функции (RBF), и сигмоидальные ядра.
Процесс обучения SVM включает в себя нахождение оптимальной гиперплоскости путем решения оптимизационной задачи. Оптимизационная задача SVM стремится максимизировать зазор и, одновременно, минимизировать ошибки классификации. Если данные не могут быть линейно разделены в исходном пространстве признаков, ядро используется для перехода в пространство более высокой размерности, где разделение становится возможным.
SVM обладает несколькими преимуществами, такими как хорошая обобщающая способность и эффективность в пространствах высокой размерности. Однако, выбор подходящего ядра и настройка гиперпараметров могут потребовать некоторого тщательного анализа данных.
Пример реализации с использованием библиотеки sklearn
# Импортируем необходимые библиотеки
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report
# Загружаем набор данных Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Разделяем данные на обучающий и тестовый наборы
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Масштабируем данные
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Создаем объект SVM
svm_classifier = SVC(kernel='linear', C=1.0, random_state=42)
# Обучаем модель на обучающем наборе
svm_classifier.fit(X_train, y_train)
# Делаем предсказания на тестовом наборе
y_pred = svm_classifier.predict(X_test)
# Оцениваем точность модели
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
# Выводим отчет о классификации
print('\nClassification Report:\n', classification_report(y_test, y_pred))В этом примере мы:
Загружаем набор данных Iris и разделяем его на обучающий и тестовый наборы.
Масштабируем данные для улучшения производительности SVM.
Создаем объект SVM с линейным ядром и параметром регуляризации C равным 1.0.
Обучаем модель на обучающем наборе данных.
Делаем предсказания на тестовом наборе данных.
Оцениваем точность модели и выводим отчет о классификации.
Обратите внимание, что в этом примере используется линейное ядро (kernel='linear'). Для более сложных задач, где данные не могут быть линейно разделены, можно использовать другие ядра, такие как радиально-базисные функции (kernel='rbf').
Пример реализации без использования библиотек
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
class SVM:
def __init__(self, learning_rate=0.01, lambda_param=0.01, n_iterations=1000):
self.learning_rate = learning_rate
self.lambda_param = lambda_param
self.n_iterations = n_iterations
self.weights = None
self.bias = None
def fit(self, X, y):
n_samples, n_features = X.shape
# Инициализация параметров
self.weights = np.zeros(n_features)
self.bias = 0
# Градиентный спуск для обучения весов
for _ in range(self.n_iterations):
model = np.dot(X, self.weights) + self.bias
hinge_loss = 1 - y * model
gradient_weights = np.zeros(n_features)
gradient_bias = 0
# Обновление весов на основе градиента
for i in range(n_samples):
if hinge_loss[i] > 0:
gradient_weights -= y[i] * X[i]
gradient_bias -= y[i]
gradient_weights = gradient_weights / n_samples + 2 * self.lambda_param * self.weights
gradient_bias = gradient_bias / n_samples
self.weights -= self.learning_rate * gradient_weights
self.bias -= self.learning_rate * gradient_bias
def predict(self, X):
model = np.dot(X, self.weights) + self.bias
return np.sign(model)
# Загрузка данных Iris
iris = datasets.load_iris()
X = iris.data
y = np.where(iris.target == 0, -1, 1) # Бинарная классификация: setosa (-1) или не setosa (1)
# Разделяем данные на обучающий и тестовый наборы
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # random_state=42
# Масштабируем данные
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Создаем и обучаем модель SVM
svm_model = SVM(learning_rate=0.01, lambda_param=0.01, n_iterations=1000)
svm_model.fit(X_train, y_train)
# Делаем предсказания на тестовом наборе данных
y_pred = svm_model.predict(X_test)
# Оцениваем точность модели
accuracy = np.mean(y_pred == y_test)
print(f'Accuracy: {accuracy:.2f}')
print("Weights:", svm_model.weights)
print("Bias:", svm_model.bias)
print("Test:", y_test)
print("Predictions:", y_pred)В этом примере мы преобразовали задачу многоклассовой классификации в задачу бинарной классификации для цветка setosa против всех остальных.
Деревья решений
Определение и построение
Дерево решений — это модель машинного обучения, используемая для принятия решений. Она представляет собой структуру древовидного вида, в которой каждый узел представляет собой тест на признаке (или атрибуте), каждая ветвь представляет собой результат этого теста, а каждый лист дерева представляет собой конечное решение, метку класса или числовое значение. Построение дерева происходит путем разделения данных на подмножества на основе значений признаков.
Процесс построения дерева решений осуществляется с использованием алгоритма, который выбирает признаки и их пороги таким образом, чтобы максимизировать информационный выигрыш или уменьшение неопределенности (например, энтропии) при каждом разделении. Рекурсивно повторяя этот процесс, строится древовидная структура, которая лучше всего описывает зависимости в данных.
Визуализация принятия решений
Визуализация принятия решений в деревьях происходит следующим образом:
- Узлы (условия):
- Узлы дерева представляют собой тесты на признаках. Например, “Длина лепестка <= 2.5” может быть узлом, проверяющим условие о длине лепестка для решения о направлении дерева.
- Ветви (решения):
- Ветви дерева представляют собой возможные результаты тестов. В случае “Длина лепестка <= 2.5” две ветви могут быть “Да” и “Нет”, указывая на два подмножества данных в зависимости от результата теста.
- Листья (конечные решения):
- Листья представляют собой конечные решения или классы. Например, в случае классификации лепесток “Да” может быть, например, “Тип цветка: Ирис версиколор”, а “Нет” может быть “Тип цветка: Ирис сетоса”.
Пример:
В этом примере дерево решений разделяет данные по признаку “Длина лепестка”. Если длина лепестка меньше или равна 2.5, то принимается решение “Тип цветка: A”. В противном случае, проверяется условие “Длина лепестка <= 5.0”. Если это условие выполняется, решение - “Тип цветка: B”, иначе - “Тип цветка: C”. Таким образом, дерево решений предоставляет структурированный и легко интерпретируемый способ принятия решений на основе признаков данных.
Проектирование и обучение моделей машинного обучения
Описание
Проектирование и обучение моделей машинного обучения — это процесс, включающий в себя несколько этапов, начиная с постановки задачи и заканчивая тестированием и оптимизацией. Вот общий обзор этапов этого процесса:
- Постановка задачи:
- Определите цель вашей модели: классификация, регрессия, кластеризация, детекция объектов и т. д.
- Определите, какие данные вам нужны для обучения и оценки модели.
- Сбор данных:
- Соберите или получите данные, необходимые для обучения и тестирования модели.
- Проверьте данные на наличие ошибок, выбросов, пропущенных значений.
- Подготовка данных:
- Выполните предобработку данных: масштабирование, нормализация, обработка выбросов, заполнение пропущенных значений.
- Разделите данные на обучающую, валидационную и тестовую выборки.
- Выбор модели:
- Выберите тип модели в соответствии с постановкой задачи.
- Рассмотрите различные архитектуры моделей и их гиперпараметры.
- Обучение модели:
- Инициализируйте модель и определите функцию потерь (loss function).
- Выберите оптимизатор и метод обучения.
- Обучите модель на обучающей выборке.
- Оцените производительность модели на валидационной выборке и внесите коррективы при необходимости.
- Оценка модели:
- Оцените производительность модели на тестовой выборке.
- Используйте метрики оценки, соответствующие вашей задаче (например, точность, F1-мера, среднеквадратичная ошибка).
- Анализируйте результаты и идентифицируйте возможные улучшения.
- Тонкая настройка (Fine-Tuning):
- Осуществите тонкую настройку модели, изменяя гиперпараметры или архитектуру для достижения лучшей производительности.
- Обратите внимание на возможное переобучение (overfitting) и принимайте меры для его предотвращения.
- Внедрение и масштабирование:
- Внедрите модель в окружение, где она будет использоваться.
- Оптимизируйте модель для эффективной работы в условиях реального времени, если это необходимо.
- Мониторинг и обновление:
- Установите механизмы мониторинга производительности модели в реальном времени.
- Периодически обновляйте модель, обучая ее на новых данных для поддержания актуальности.
Этот процесс является итеративным, и может потребоваться несколько циклов, чтобы достичь оптимальных результатов. Каждый этап требует внимания и экспертного анализа для того, чтобы создать эффективную и точную модель машинного обучения.
Оценка моделей и переобучение
Метрики оценки моделей
1. Точность (Accuracy):
- Определение: Доля правильных ответов модели среди всех предсказаний.
- Формула: \(\frac{{TP + TN}}{{TP + TN + FP + FN}}\)
- Примечание: Хороша для сбалансированных классов, но может быть обманчива при несбалансированных классах.
2. Полнота (Recall или Sensitivity):
- Определение: Доля правильно предсказанных положительных случаев относительно всех реальных положительных случаев.
- Формула: \(\frac{{TP}}{{TP + FN}}\)
- Примечание: Важна в задачах, где пропуск положительных случаев нежелателен (например, в медицинских диагнозах).
3. F1-мера:
- Определение: Сбалансированная метрика, объединяющая точность и полноту.
- Формула: \(2 \cdot \frac{{\text{{Precision}} \cdot \text{{Recall}}}}{{\text{{Precision}} + \text{{Recall}}}}\)
- Примечание: Хороша для задач с неравномерными классами.
4. ROC-кривые и AUC-ROC:
- ROC-кривая: График, отображающий зависимость True Positive Rate (Recall) от False Positive Rate для различных значений порога классификации.
- AUC-ROC (Area Under the ROC Curve): Площадь под ROC-кривой, представляющая общую производительность модели.
- Интерпретация: Чем выше AUC-ROC, тем лучше модель способна различать классы. AUC-ROC равен 1 для идеальной модели и 0.5 для случайного классификатора.
Пример кода для вычисления метрик в Python:
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve, auc
import matplotlib.pyplot as plt
# Пример истинных меток и предсказанных вероятностей
y_true = [1, 0, 1, 1, 0, 1, 0, 0, 1, 0]
y_pred_prob = [0.8, 0.3, 0.6, 0.7, 0.2, 0.9, 0.1, 0.4, 0.75, 0.3]
# Преобразование вероятностей в бинарные предсказания
y_pred = [1 if prob >= 0.5 else 0 for prob in y_pred_prob]
# Вычисление метрик
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
roc_auc = roc_auc_score(y_true, y_pred_prob)
# Вывод метрик
print(f"Accuracy: {accuracy:.4f}")
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")
print(f"F1 Score: {f1:.4f}")
print(f"AUC-ROC: {roc_auc:.4f}")
# Построение ROC-кривой
fpr, tpr, thresholds = roc_curve(y_true, y_pred_prob)
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'AUC = {roc_auc:.2f}')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()Accuracy: 1.0000
Precision: 1.0000
Recall: 1.0000
F1 Score: 1.0000
AUC-ROC: 1.0000Проблема переобучения
Причины переобучения
- Слишком сложная модель:
- Использование сложных моделей с большим числом параметров может привести к тому, что модель слишком точно подстроится под тренировочные данные, включая шум и случайные особенности.
- Недостаточное количество данных:
- Когда количество данных недостаточно для обучения сложных моделей, модель может “запомнить” тренировочный набор вместо того, чтобы обобщать паттерны.
- Переизбыток признаков:
- Включение избыточных признаков, особенно если они неинформативны или коррелируют между собой, может привести к переобучению.
Способы предотвращения переобучения
- Упрощение модели:
- Использование более простых моделей с меньшим числом параметров может снизить риск переобучения. Например, использование модели линейной регрессии вместо сложных алгоритмов.
- Регуляризация:
- Применение техник регуляризации, таких как L1 или L2 регуляризация, может помочь уменьшить веса параметров, предотвращая их переобучение.
- Увеличение объема данных:
- Добавление большего количества разнообразных данных может помочь модели лучше обобщать паттерны, а не переобучаться на ограниченном наборе данных.
- Кросс-валидация:
- Использование кросс-валидации может помочь в оценке производительности модели на различных подмножествах данных, что позволяет выявить переобучение.
- Отбор признаков:
- Исключение ненужных или коррелирующих признаков может уменьшить риск переобучения.
- Сбор данных:
- Сбор большего объема данных, особенно если они разнообразны и представляют различные сценарии, может помочь в построении более устойчивой и обобщающей модели.
Роль кросс-валидации
Кросс-валидация — это метод, который используется для оценки производительности модели, особенно когда у вас ограниченный объем данных. Он включает разделение данных на несколько подмножеств (фолдов), обучение модели на одном подмножестве и тестирование на другом. Процесс повторяется несколько раз, и результаты усредняются.
Роль кросс-валидации в предотвращении переобучения:
- Кросс-валидация позволяет оценить, как хорошо модель обобщает паттерны на различных подмножествах данных. Если модель проявляет высокую производительность на тренировочных данных, но низкую на тестовых данных, это может свидетельствовать о переобучении. Кросс-валидация помогает выявить такие проблемы и настраивать параметры модели для улучшения ее обобщающей способности.
Библиотеки и инструменты
Python и библиотеки для машинного обучения
Python является одним из самых популярных языков программирования для разработки машинного обучения. Его популярность обусловлена несколькими факторами:
Обширная экосистема библиотек: Python имеет обширную и активно развивающуюся экосистему библиотек, специализированных на машинном обучении и искусственном интеллекте.
Простота и читаемость кода: Python обладает чистым и понятным синтаксисом, что облегчает разработку и поддержку кода.
Множество инструментов и фреймворков: Существует множество инструментов и фреймворков для разработки, тестирования и развертывания моделей машинного обучения.
Активное сообщество: Python имеет активное сообщество разработчиков, что способствует обмену знаний, решению проблем и появлению новых инструментов.
Обзор популярных библиотек
- scikit-learn:
- Описание: scikit-learn предоставляет простой и эффективный набор инструментов для анализа данных и построения моделей машинного обучения. Он включает в себя алгоритмы для классификации, регрессии, кластеризации, обработки текста, извлечения признаков и др.
- Применение: Подходит для начинающих и опытных разработчиков, легко использовать и поддерживать.
- TensorFlow:
- Описание: TensorFlow — это открытая библиотека для числовых вычислений, которая широко используется в разработке моделей глубокого обучения. Он обеспечивает гибкость и масштабируемость для разработки разнообразных моделей.
- Применение: Широко используется для разработки и обучения нейронных сетей.
- PyTorch:
- Описание: PyTorch также предоставляет инструменты для работы с нейросетями и глубоким обучением. Отличается динамическим вычислением графа, что облегчает отладку и экспериментирование.
- Применение: Часто используется исследователями в области искусственного интеллекта и глубокого обучения.
Каждая из этих библиотек имеет свои особенности и применение в зависимости от конкретных задач и предпочтений разработчика. Важно выбирать библиотеку в соответствии с требованиями проекта и уровнем опыта команды.
Среды разработки и инструменты
Jupyter Notebooks и их роль в обучении
Jupyter Notebooks представляют собой интерактивную среду программирования, которая позволяет объединить код, текстовую информацию и визуализации в одном документе. В области обучения и разработки машинного обучения Jupyter Notebooks играют ключевую роль по нескольким причинам:
Интерактивная разработка: Jupyter Notebooks позволяют разрабатывать и тестировать код пошагово, исполняя ячейки поочередно. Это особенно полезно при обучении, поскольку позволяет студентам и исследователям наблюдать результаты шаг за шагом, что способствует лучшему пониманию кода и алгоритмов.
Интеграция кода и текста: В Jupyter Notebooks можно вставлять текстовые ячейки с описанием шагов, комментариями и формулировками задач. Это упрощает создание интерактивных учебных материалов и делает код более доступным.
Визуализация данных: В Jupyter Notebooks легко создавать и визуализировать графику, диаграммы и графы прямо в документе. Это облегчает анализ данных и демонстрацию результатов.
Обмен знаний и репродуцируемость: Jupyter Notebooks могут быть легко обменены между исследователями и студентами. Это способствует репродуцируемости результатов и обеспечивает прозрачность в процессе исследования.
Поддержка множества языков программирования: Jupyter поддерживает несколько языков программирования, включая Python, R, Julia и другие. Это позволяет использовать Jupyter для различных задач и предпочтений.
Интерактивные среды для визуализации данных
В дополнение к Jupyter Notebooks, существует ряд интерактивных сред разработки и визуализации данных, таких как:
Matplotlib: Это библиотека визуализации данных для создания статических, анимированных и интерактивных графиков в Python.
Seaborn: Это высокоуровневая библиотека для визуализации данных на основе Matplotlib, предоставляющая более простой интерфейс и более красочие стандартные стили.
Plotly: Позволяет создавать интерактивные графики, диаграммы и даже трехмерные визуализации.
Bokeh: Обеспечивает создание интерактивных графиков веб-приложений, которые могут быть встроены в Jupyter Notebooks.
Эти инструменты помогают визуализировать данные, делать их более понятными и облегчать анализ результатов в машинном обучении и других областях.