Лаб. работа “Методы одномерной оптимизации”

Разработка и оптимизация интеллектуальных информационных систем

Практика

Автор

Бизюк Андрей

Дата публикации

29 февраля 2024 г.

Постановка задачи

Найти точку минимума функции с заданной погрешностью

\[ f(x)=(x-8)^2-7 \]

Локализация экстремума

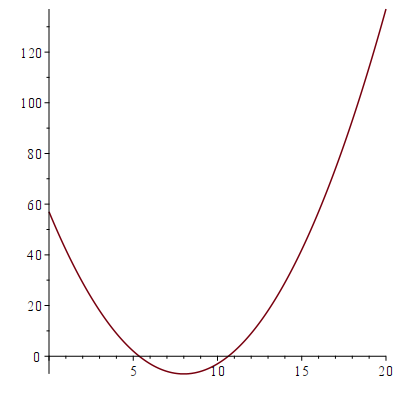
Определим отрезок, на котором находится точка минимума

Функция имеет единственную точку минимума на отрезке \([0;20]\)

Метод оптимального пассивного поиска

Для решения задачи методом оптимального пассивного поиска будем использовать MsExcel или LibreOffice.

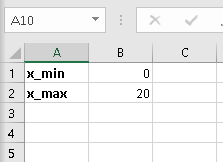
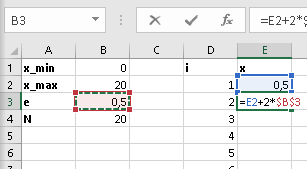
Зададим исходные данные

Необходимо выбрать погрешность поиска точки минимума. От выбора погрешности зависит количество точек, в которых нужно будет найти значение функции.

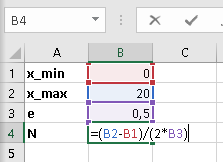
Выберем погрешность \(\epsilon = 0.5\). Количество точек найдем по формуле \(N=\frac{x_{max}-x_{min}}{2\epsilon}=\frac{20-0}{2\times 0.5}=20\)

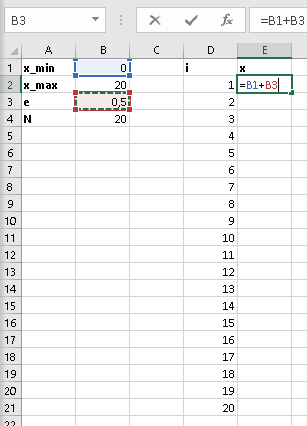
Выберем точки \(x_i,\ i=1..N\), в которых нужно найти значение функции. Согласно методу оптимального пассивного поиска, точка \(x_1\) должна иметь координату \(x_{min}+\epsilon\). Остальные точки находятся по формуле: \(x_i=x_{i-1}+2\epsilon,\ i=2..N\).

Найдем значение функции для всех \(x_i\):

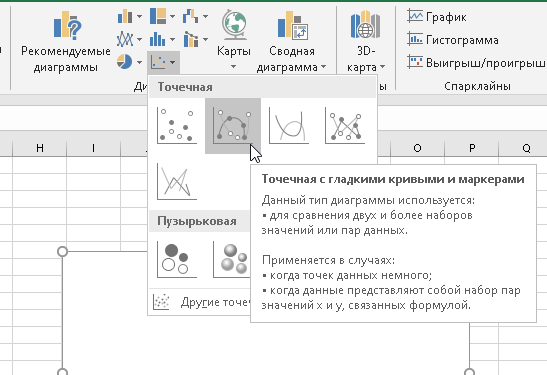
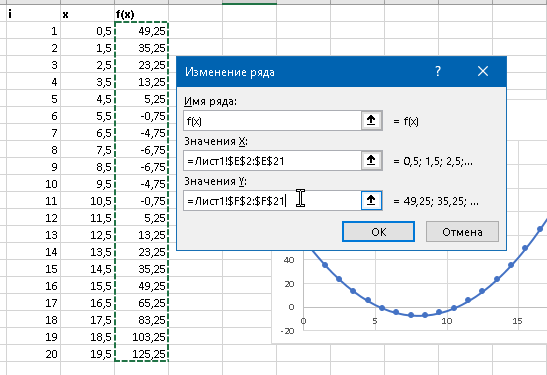
Построим график \(f(x)\) по полученным данным. Нужно вставить диаграмму точечного типа, а затем выбрать данные для нее.

Определим точку минимума и минимальное значение функции. Напишем формулы, которые найдут эти значения автоматически. Для этого нам потребуются функции МИН, ПОИСКПОЗ и ИНДЕКС.

Таким образом мы получили следующее решение:

\[ x_{opt}=7.5,\ f(x_{opt})=-6.75 \]

Найденное значение \(x_{opt}\) отличается от истинной точки минимума \(x^*=8\) на величину, не превышающую \(\epsilon\), следовательно, мы выполнили условие задачи.

Метод дихотомии

Для решения задачи методом дихотомии, необходимо написать программу, реализующую этот алгоритм.

Приведем пример реализации алгоритма метода дихотомии в виде рекурсивной функции в среде Maple:

dichotomy := proc(a, b, f, delta, eps)
local x1, x2; global count; 
if b - a < eps then return a; end if; 
count := count + 2; 
x1 := 1/2*a + 1/2*b - delta; 
x2 := 1/2*a + 1/2*b + delta; 
if f(x2) < f(x1) then 
  return dichotomy(x1, b, f, delta, eps); 
end if; 
return dichotomy(a, x2, f, delta, eps); 
end proc:

Пример использования этой функции для решения задачи поиска точки минимума функции:

f := x -> (x - 8)^2 - 7:
a := 0:
b := 20:
count := 0:
epsilon := 0.001:
delta := 0.00001:
x_o := dichotomy(a, b, f, delta, epsilon):
x_opt = x_o;
f_opt = f(x_o);
N = count;
 
#                      x_opt = 7.999869929
#                      f_opt = -6.999999983
#                             N = 30

Метод золотого сечения

Приведем пример реализации алгоритма метода золотого сечения в виде рекурсивной функции в среде Maple:

goldenratio := proc(a, b, f, x, y, n, eps) 
local x1, x2, f1, f2; global count; 
if b - a < eps then return a; end if;
count := count + 1;

if n = 1 then 
    x1 := b + a - x; 
    x2 := x; 
    f1 := f(x1); 
    f2 := y; 
else 
    x1 := x; 
    x2 := b + a - x; 
    f1 := y; 
    f2 := f(x2); 
end if; 

if evalf(f2) < evalf(f1) then 
    return goldenratio(x1, b, f, x2, f2, 2, eps);
end if;
return goldenratio(a, x2, f, x1, f1, 1, eps);
end proc:

Пример использования этой функции для решения задачи поиска точки минимума функции:

f := x -> (x - 8)^2 - 7:
tau := (1 + sqrt(5))/2:
a := 0:
b := 20:
x1 := evalf((b + a*(tau - 1))/tau):
count := 1:
goldenratio(a, b, f, x1, f(x1), 1, 0.001);
count;
#                           7.99948468
#                              22

Метод Фибоначчи

Приведем пример реализации алгоритма метода Фибоначчи в виде рекурсивной функции в среде Maple:

fibonacciseries := proc(n) 
local s, i; 
s := [1, 1]; 
for i from 3 to n do 
    s := [op(s), s[i - 1] + s[i - 2]]; 
end do; 
return s; 
end proc:

fibonacci := proc(a, b, f, x, y, n, s, l)
local x1, x2, f1, f2; global count;
if count >= nops(s) - 2 then return evalf(a); end if;
count := count + 1;
if n = 1 then
    x1 := a + l*s[nops(s) - count - 1]/s[nops(s)];
    x2 := x; f1 := f(x1);
    f2 := y;
else
    x1 := x;
    x2 := a + l*s[nops(s) - count]/s[nops(s)];
    f1 := y; f2 := f(x2);
end if;

if evalf(f2) < evalf(f1) then
    return fibonacci(x1, b, f, x2, f2, 2, s, l);
else
    return fibonacci(a, x2, f, x1, f1, 1, s, l);
end if;
end proc:

Пример использования этой функции для решения задачи поиска точки минимума функции:

f := x -> (x - 8)^2 - 7:
s2 := fibonacciseries(24);
x1 := a + (b - a)*s2[(nops(s2) - 1) - 1]/s2[nops(s2)]:
count := 1:
a := 0:
b := 20:
fibonacci(a, b, f, x1, f(x1), 1, s2, b - a);
count;

# s2 := [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368]
#                          7.999482402
#                              22

Варианты индивидуальных заданий

\(f(x) = x^2 + 3x + 2\)
\(f(x) = e^{0.5x} - 2x\)
\(f(x) = \sin(2x) + x\)
\(f(x) = -\ln(2x + 1)+x\)
\(f(x) = 2x^3 - 5x^2 + x + 3\)
\(f(x) = -\sqrt{3x} + x\)
\(f(x) = \cos(2x) + \frac{1}{x+1}\)
\(f(x) = x \cdot \ln(0.5x + 1)\)
\(f(x) = 3x^3 - 2x^2 + 4x - 1\)
\(f(x) = \frac{1}{2}x^2 - 2x + 4\)
\(f(x) = e^{-0.5x} + \cos(x)\)
\(f(x) = \frac{1}{x^2} + 2x + 1\)
\(f(x) = \tan(0.5x) + x^2\)
\(f(x) = \frac{1}{x} + \sqrt{2x}\)
\(f(x) = \sinh(0.5x) + 0.5x\), где \(\sinh(x)=\frac{e^x-e^{-x}}{2}\)

Наверх