Лаб. работа “Методы многомерной оптимизации”
Теоретическая информация
Отделение точки минимума
Перед поиском точки минимума, нужно найти ее окрестность. Методы спуска будут давать надежные результаты только если начальная точка будет выбрана достаточно близко от точки минимума.
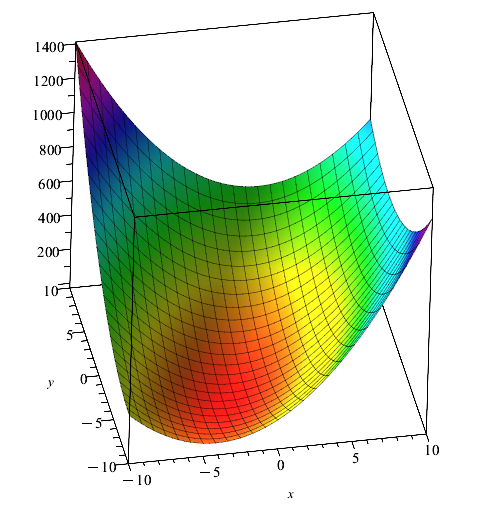
Если функция двумерная, то для определения окрестности точки минимума, можно построить ее график.
Пример построения графика функции в среде Maple:
with(plots):
f := (x1, x2) -> 6*x1^2 - 4*x2*x1 + 3*x2^2 + 4*sqrt(5)*(2*x2 + x1) + 22: #Функция
plot3d(f(x,y),x=-10..10,y=-10..10,colorscheme = ["zcoloring",z->z]);Результат:
Проанализировав график функции, можем выбрать в качестве начальной точки точку [-2,1] .
Метод градиентного спуска
Метод градиентного спуска является одним из наиболее распространенных методов оптимизации для поиска минимума функции. В случае двумерных функций, где у вас есть две независимых переменных (\(x\) и \(y\)), вы можете использовать следующий алгоритм для минимизации функции:
Инициализация: Выберите начальное приближение \((x_0, y_0)\) в области, где вы хотите найти минимум функции. Обычно начальная точка выбирается произвольно, но может повлиять на скорость сходимости.
Вычисление градиента: Найдите градиент функции в текущей точке \((x, y)\). Градиент - это вектор, который указывает на направление наибольшего возрастания функции.
Градиент функции \(f(x, y)\) вычисляется следующим образом:
Градиент \(f(x, y) = (∂f/∂x, ∂f/∂y)\)
Где \(∂f/∂x\) и \(∂f/∂y\) - частные производные функции \(f\) по переменным \(x\) и \(y\) соответственно.
Шаг градиентного спуска: Обновите текущее приближение \((x, y)\) в направлении, противоположном градиенту, чтобы уменьшить значение функции. Это делается путем вычитания градиента, умноженного на некоторую константу, называемую скоростью обучения (learning rate), обозначаемой как \(\alpha\).
Новое приближение:
\(x_{new} = x - \alpha \cdot ∂f/∂x\)
\(y_{new} = y - \alpha \cdot ∂f/∂y\)
Повторение: Повторяйте шаги 2 и 3, пока не достигнете условия остановки. Это может быть заданным количеством итераций или до тех пор, пока изменение функции не станет малым.
Скорость обучения (learning rate) является важным гиперпараметром метода градиентного спуска. Если он выбран слишком большим, то сходимость может быть нестабильной, а если слишком маленьким, то метод может сходиться очень медленно. Экспериментирование с различными значениями скорости обучения может потребоваться для достижения оптимальной сходимости.
Таким образом, метод градиентного спуска позволяет находить минимум двумерных функций путем постепенного движения в направлении наибольшего убывания функции (градиента).
Пример реализации в среде Maple
Процедура метода градиентного спуска:
gd:=proc(df,x0,eps,alpha,maxn)
local X,G,Xk,i,modgrad;
X:=[x0];
G := [1, 1];
modgrad := g -> evalf(sqrt(g[1]^2 + g[2]^2));
for i while eps < modgrad(G) and nops(X) < maxn do
G := df(X[i][1], X[i][2]);
Xk := [0, 0];
Xk := evalf(-G*alpha + X[i]);
X := [op(X), Xk] ;
end do;
return X;
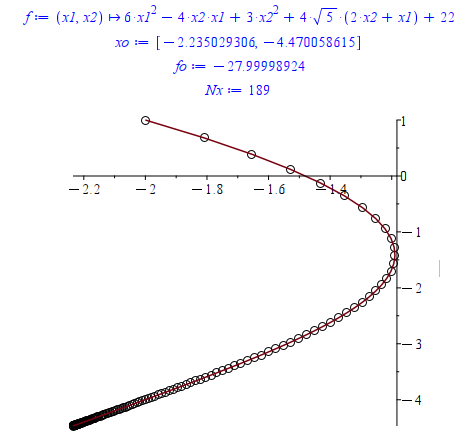
end proc:Пример использования для оптимизации функции:
with(plots):
f := (x1, x2) -> 6*x1^2 - 4*x2*x1 + 3*x2^2 + 4*sqrt(5)*(2*x2 + x1) + 22; #Функция
df := (x1, x2) -> [D[1](f)(x1, x2), D[2](f)(x1, x2)]: #Частные производные
eps := 0.01: #Погрешность
alpha := 0.01: #Коэффициент шага градиентного спуска
maxn := 1000: #Максимальное количество итераций
x0 := [-2, 1]: #Начальная точка
X := gd(df, x0, eps, alpha, maxn): #Запуск метода и получение последовательности точек
xo := X[nops(X)]; #Точка минимума
fo := evalf(eval(f(x1, x2), {x1 = xo[1], x2 = xo[2]})); #Минимальное значение функции
Nx:=nops(X); #Количество точек
display(pointplot(X, symbol = circle, symbolsize = 20), plot(X)); #Построение графика по точкамРезультат:
Метод градиентного спуска с дроблением шага
Дробление шага (или уменьшение шага) - это метод, который может использоваться в методе градиентного спуска для улучшения его сходимости. Он помогает настроить скорость обучения (learning rate) так, чтобы метод сходился быстро и стабильно. Этот метод включает в себя постепенное уменьшение значения скорости обучения по ходу итераций. Вот как это работает:
Инициализация: Выберите начальное значение скорости обучения (например, \(\alpha = 0.1\)) и начальное приближение \((x_0, y_0)\).
Вычисление градиента: Найдите градиент функции в текущей точке \((x, y)\).
Шаг градиентного спуска: Обновите текущее приближение \((x, y)\) в направлении, противоположном градиенту, используя текущее значение скорости обучения.
Уменьшение скорости обучения:
Критерий дробления шага в методе градиентного спуска основан на неравенстве, которое позволяет определить, когда нужно уменьшить скорость обучения (learning rate). Обычно используется неравенство на изменение функции потерь (или целевой функции) между текущей и следующей итерациями. Это неравенство может быть сформулировано следующим образом:
Если \(f(x_{k+1}) ≤ f(x_k) - \alpha \cdot β \cdot ||∇f(x_k)||^2\),
где:
- \(f(x_k)\) - значение функции потерь (или целевой функции) на текущей итерации \(k\),
- \(f(x_{k+1})\) - значение функции потерь на следующей итерации \(k+1\) (после обновления параметров),
- \(\alpha\) - скорость обучения (learning rate),
- \(β\) - некоторая константа между 0 и 1,
- \(||∇f(x_k)||^2\) - квадрат нормы градиента функции на текущей итерации.
Суть этого неравенства заключается в том, что скорость обучения уменьшается, если значение функции потерь на следующей итерации оказывается больше, чем значение функции потерь на текущей итерации, учитывая величину градиента. Таким образом, если изменение функции потерь оказывается маленьким, то можно увеличить скорость обучения. В противном случае, если изменение функции потерь слишком большое, уменьшение скорости обучения помогает предотвратить расходимость метода.
Значения констант \(\alpha\) и \(β\) могут быть настроены в зависимости от конкретной задачи и оптимизационного метода. Это неравенство позволяет учесть историю изменения функции потерь и градиента при выборе скорости обучения, что делает метод градиентного спуска более адаптивным к различным условиям и задачам.
Повторение: Повторяйте шаги 2 - 4 до тех пор, пока не достигнете условия остановки.
Преимущество дробления шага заключается в том, что он позволяет начать с большей скоростью обучения, которая может ускорить начальную сходимость, а затем уменьшать ее по мере приближения к минимуму. Это позволяет избежать проблемы выбора постоянно маленького значения скорости обучения, которое может замедлить сходимость метода.
Однако важно следить за тем, чтобы коэффициент уменьшения скорости обучения (например, 0.9) был разумным, чтобы не слишком быстро уменьшать скорость обучения и не пропустить оптимум. Этот коэффициент может потребовать настройки в зависимости от конкретной задачи.
Пример реализации в среде Maple
Процедура градиентного спуска с дроблением шага:
gd:=proc(f,df,x0,eps,alpha,beta,gamma,maxn)
local X,G,Xk,i,j,modgrad,_alpha,A;
X:=[x0];
G := [1, 1];
A := [alpha];
modgrad := g -> evalf(sqrt(g[1]^2 + g[2]^2));
for i while eps < modgrad(G) and nops(X) < maxn do
G := df(X[i][1], X[i][2]);
Xk := [0, 0];
_alpha := alpha;
Xk := evalf(-G*alpha + X[i]);
for j while evalf(f(X[i][1], X[i][2]) - f(Xk[1], Xk[2])) < evalf(_alpha*beta*modgrad(G)^2) do
_alpha := _alpha*gamma;
A := [op(A), _alpha];
Xk := evalf(-G*_alpha + X[i]);
end do;
X := [op(X), Xk];
end do;
return X;
end proc:Пример использования для оптимизации функции:
with(plots):
f := (x1, x2) -> 6*x1^2 - 4*x2*x1 + 3*x2^2 + 4*sqrt(5)*(2*x2 + x1) + 22; #Функция
df := (x1, x2) -> [D[1](f)(x1, x2), D[2](f)(x1, x2)]: #Частные производные
eps := 0.01: #Погрешность
alpha := 10: #Коэффициент шага градиентного спуска
beta := 0.5: #Коэффициент сходимости
gamma_ := 0.8: #Коэффициент дробления шага
maxn := 1000: #Максимальное количество итераций
x0 := [-2, 1]: #Начальная точка
X := gd(f,df, x0, eps, alpha, beta, gamma_, maxn): #Запуск метода и получение последовательности точек
xo := X[nops(X)]; #Точка минимума
fo := evalf(eval(f(x1, x2), {x1 = xo[1], x2 = xo[2]})); #Минимальное значение функции
Nx:=nops(X); #Количество точек
display(pointplot(X, symbol = circle, symbolsize = 20), plot(X)); #Построение графика по точкамРезультат:
Ответ методом градиентного спуска с дроблением шага получен за меньшее число шагов.
Метод поиска по шаблону
Метод поиска по шаблону (Pattern Search) - это один из численных методов оптимизации, который может использоваться для поиска минимума многомерной функции. В этом методе используется некоторый шаблон, который представляет собой набор точек в многомерном пространстве, и основная идея заключается в поиске лучшей точки в этом шаблоне, которая минимизирует целевую функцию.
Инициализация:
Начальная точка: Выберите начальную точку в многомерном пространстве. Это будет ваша первая текущая точка.
Размер шаблона: Определите размер шаблона, который представляет собой n-мерный куб с центром в текущей точке. Размер шаблона важен, так как он будет влиять на область поиска.
Шаг поиска: Задайте шаг для поиска в каждом направлении. Этот шаг будет определять, насколько далеко вы будете исследовать окрестности текущей точки.
Оценка целевой функции:
- Вычислите значение целевой функции в центре шаблона и в его угловых точках. Это означает, что вы должны вычислить значение функции в текущей точке и в её ближайших соседях в многомерном пространстве.
Поиск лучшей точки:
- Найдите точку с наименьшим значением целевой функции в шаблоне. Эта точка становится новой текущей точкой.
Шаг обновления:
- Обновите шаблон, перемещая его центр к новой текущей точке. Это означает, что ваш шаблон будет центрирован вокруг новой текущей точки.
Критерий остановки:
- Повторяйте шаги 2 - 4 до тех пор, пока не выполнится какой-то критерий остановки, например:
- Достижение максимального числа итераций.
- Сходимость, когда изменение текущей точки становится незначительным.
- Достижение заданного уровня точности (значения функции близкого к минимуму).
- Повторяйте шаги 2 - 4 до тех пор, пока не выполнится какой-то критерий остановки, например:
Вывод:
- Как только метод сойдется, текущая точка будет приближением к минимуму функции.
Важно подобрать размер шаблона и шаг поиска так, чтобы адаптировать метод к конкретной задаче. Слишком маленький шаблон может привести к застреванию в локальных минимумах, а слишком большой шаблон может замедлить сходимость метода.
Метод поиска по шаблону полезен в тех случаях, когда целевая функция может быть шумной или содержать локальные минимумы, и когда нет информации о производных функции (как в методах градиентного спуска).
Пример реализации в среде Maple
Функции:
# вычисляет координаты вершин куба с заданным центром
# и длиной ребра
# l - длина ребра
# center - центр куба
# dims - размерность пространства
cube:=proc(l,center,dims:=2);
local i,j,n,nvert,verts;
nvert:=2^dims;
verts:=Array(1..nvert,1..dims);
for i from 0 to nvert-1 do
n:=i;
for j from dims-1 to 0 by -1 do
if irem(n,2,'n') = 0 then
verts[i+1,j+1] := center[j+1] - l/2.0;
else
verts[i+1,j+1] := center[j+1] + l/2.0;
end if;
end do;
end do:
return verts;
end proc:
# вычисляет значение функции в вершинах куба
# f - функция
# cube - массив с координатами вершин куба
mapcube:=proc(f,cube);
local n,i,fs;
n:=upperbound(cube)[1]:
fs:=Array(1..n):
for i from 1 to n do
fs(i):=f(op(convert(cube[i],list))):
end do:
return fs:
end proc:
# сравнивает значение функции в центре куба со
# значениями в вершинах и возвращает номер минимальной или -1
# если значение во всех вершинах >= чем в центре
# fcenter - значение функции в центре
# fcube - массив из значений функции в вершинах
find_opt_vert:=proc(fcenter,fcube):
local i,result,n,minf:
result:=-1:
minf:=fcenter:
n:=upperbound(fcube):
for i from 1 to n do
if minf >= fcube[i] then
minf:=fcube[i]:
result:=i:
end if:
end do:
return result:
end proc:
# ищет минимум функции используя шаблонный поиск
# dims - размерность задачи
# f - функция
# start - начальная точка
# l - длина ребра куба
# centers - массив из центров кубов (out)
# cubes - массив из вершин кубов (out)
# fcenters - массив из значений функции в центрах кубов (out)
# fcubes - массив из значений функции в вершинах кубов (out)
template_search:=proc(dims,f,start,l,centers,cubes,fcenters,fcubes):
local step,optvert:
centers(1):=start:
fcenters(1):=f(op(convert(centers[1],list))):
step:=1:
while true do
cubes(step):=cube(l,centers[-1],dims):
fcubes(step):=mapcube(f,cubes[-1]);
optvert:=find_opt_vert(fcenters[-1],fcubes[-1]):
if optvert < 0 then
break;
end if:
centers(step+1):=cubes[-1][optvert]:
fcenters(step+1):=fcubes[-1][optvert]:
step++:
end do:
return step:
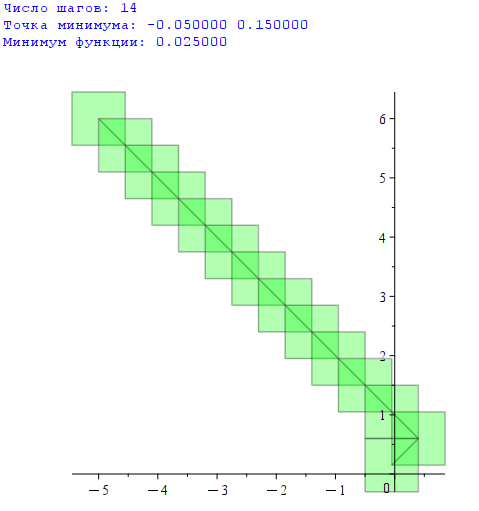
end proc:Пример использования:
with(plots):with(plottools):
dimensions:=2:
func:=(x,y)->x^2+y^2:
start:=Array([-5,6]):
l:=0.9:
centers:=Array():
cubes:=Array():
fcenters:=Array():
fcubes:=Array():
steps:=template_search(dimensions,func,start,l,centers,cubes,fcenters,fcubes):
printf("Число шагов: %d\n", steps);
printf("Точка минимума: %f\n", centers[-1]);
printf("Минимум функции: %f\n", fcenters[-1]);
display(
seq(polygon(Array(<cubes[-i][1],cubes[-i][2],cubes[-i][4],cubes[-i][3]>)),i=1..steps)
,transparency=0.7,color=green
,curve([seq(convert(centers[i],list),i=1..steps)],color=black)
);Результат:
Шаблонный поиск с редукцией
Редукция означает уменьшение длины ребра куба (например в 2 раза), при достижении окрестности точки минимума.
Редукция позволяет найти точку минимума с меньшей погрешностью, не увеличивая количество шагов алгоритма. Начальное значение длины ребра куба можно выбрать большим, чтобы первые шаги быстро приблизили поиск к точке минимума.
В данном методе есть дополнительный параметр - минимальная длина ребра куба. Этот параметр задает величину, до которой длина ребра куба может уменьшиться при редукции. Минимальная длина ребра определяет погрешность найденного решения.
Для реализации метода с редукцией, нужно добавить к предыдущему примеру новую процедуру:
# Функция ищет минимум функции используя шаблонный поиск с редукцией
# dims - размерность задачи
# f - функция
# start - начальная точка
# l - начальная длина ребра куба
# centers - массив из центров кубов (out)
# cubes - массив из вершин кубов (out)
# fcenters - массив из значений функции в центрах кубов (out)
# fcubes - массив из значений функции в вершинах кубов (out)
# lmin - минимальная длина ребра куба
template_search_reduction:=proc(dims,f,start,l,centers,cubes,fcenters,fcubes,lmin):
local step,optvert,lcur:
centers(1):=start:
fcenters(1):=f(op(convert(centers[1],list))):
lcur:=l:
step:=1:
while true do
cubes(step):=cube(lcur,centers[-1],dims):
fcubes(step):=mapcube(f,cubes[-1]);
optvert:=find_opt_vert(fcenters[-1],fcubes[-1]):
if optvert < 0 then
if lcur <= lmin then
break:
else
lcur:=lcur*0.5:
next:
end if:
end if:
centers(step+1):=cubes[-1][optvert]:
fcenters(step+1):=fcubes[-1][optvert]:
step++:
end do:
return step:
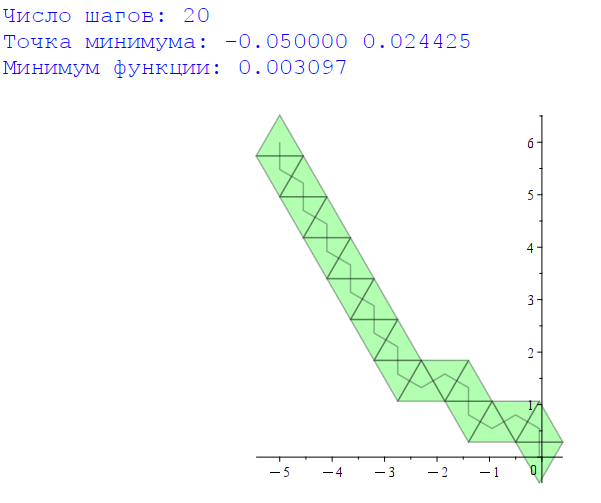
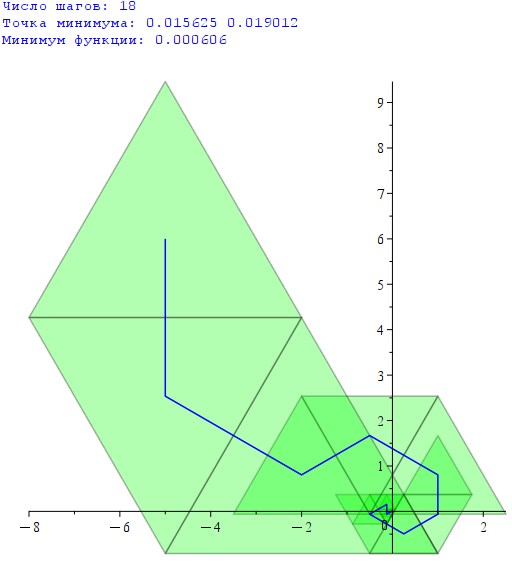
end proc:Пример использования:
with(plots):with(plottools):
dimensions:=2:
func:=(x,y)->x^2+y^2:
start:=Array([-5,6]):
l:=6:
lmin:=0.1:
centers:=Array():
cubes:=Array():
fcenters:=Array():
fcubes:=Array():
steps:=template_search_reduction(dimensions,func,start,l,centers,cubes,fcenters,fcubes,lmin):
printf("Число шагов: %d\n", steps);
printf("Точка минимума: %f\n", centers[-1]);
printf("Минимум функции: %f\n", fcenters[-1]);
display(
seq(polygon(Array(<cubes[-i][1],cubes[-i][2],cubes[-i][4],cubes[-i][3]>),
transparency=0.7,color=green),
i=1..steps)
,curve([seq(convert(centers[i],list),i=1..steps)],color=blue)
);Результат:
Метод симплексного поиска
Метод симплексного поиска с регулярным симплексом, также известный как метод Розенброка, представляет собой вариацию метода симплексного поиска, в которой симплекс остаётся регулярным (равносторонним), чтобы обеспечить лучшую сходимость и стабильность в процессе оптимизации. Этот метод обычно используется для оптимизации многомерных функций.
Основные шаги метода симплексного поиска с регулярным симплексом:
Инициализация:
Начните с выбора начальной точки и задайте размер симплекса. Обычно симплекс начинается как равносторонний многогранник, например, в n-мерном пространстве симплекс может иметь \(n + 1\) вершину.
Для создания регулярного симплекса в n-мерном пространстве с центром в заданной точке, вы можете использовать следующие формулы для вычисления координат вершин этого симплекса. Для регулярного симплекса с \(n + 1\) вершинами, каждая вершина будет равноудалена от центральной точки в разных направлениях. Предполагается, что центральная точка находится в начале координат \((0, 0, ..., 0)\).
Для вершины \(i\) симплекса, где \(i\) изменяется от \(0\) до \(n\), используйте следующие формулы:
Координаты вершины i:
\(x_i = r \cdot cos(θ_i)\), где \(r\) - радиус симплекса, \(θ_i\) - угол между вершиной \(i\) и одной из координатных осей (обычно начинают с вершины \(i\) = 0 и двигаются по часовой стрелке в n-мерном пространстве).
Для вершины \(i = 0, θ_0 = 0\).
Для вершины \(i > 0, θ_i = 2π \cdot (i - 1) / n\).
Таким образом, если у вас есть \(n + 1\) вершина симплекса, вы можете вычислить их координаты с помощью этих формул. Радиус симплекса r зависит от размера симплекса и определяется заданной длиной его ребра или другими характеристиками задачи оптимизации.
Пример для двумерного случая (\(n = 1\)): Если у вас есть регулярный симплекс с двумя вершинами, радиус r можно выбрать, например, как расстояние между вершинами. Тогда координаты вершин будут:
- Вершина 0: \((r \cdot cos(0), r \cdot sin(0)) = (r, 0)\)
- Вершина 1: \((r \cdot cos(π), r \cdot sin(π)) = (-r, 0)\)
В двумерном случае это просто линейный симплекс. В n-мерном случае вершины будут равномерно распределены вокруг начала координат в n-мерном пространстве.
Оценка целевой функции:
- Вычислите значение целевой функции в каждой из вершин симплекса. Определите, какая из вершин является наилучшей (с наименьшим значением функции), наихудшей (с наибольшим значением функции) и второй по наихудшему значению.
Рефлексия:
- Создайте новую точку, отраженную относительно наихудшей вершины относительно центра оставшихся вершин. Эта новая точка будет находиться на противоположной стороне симплекса. Если значение функции в отраженной точке меньше, чем значение в наихудшей вершине, замените наихудшую вершину этой новой точкой.
Растяжение:
- Если отраженная точка все еще лучше, чем наилучшая вершина, то попробуйте растянуть симплекс, увеличив расстояние от отраженной точки до центральной вершины симплекса. Если новая точка после растяжения также является лучше, чем наилучшая вершина, замените наихудшую вершину новой точкой.
Сжатие:
- Если отраженная точка хуже, чем вторая по наихудшему значению вершина симплекса, то можно попробовать сжать симплекс, уменьшив расстояние между наихудшей и центральной вершинами симплекса.
Уменьшение симплекса:
- Если ни один из вышеперечисленных шагов не приводит к улучшению, уменьшите размер симплекса, уменьшив расстояние между каждой вершиной симплекса и наилучшей вершиной.
Критерий остановки:
- Повторяйте шаги с 2 по 6 до выполнения критерия остановки, такого как достижение заданного числа итераций, сходимость или достижение заданного уровня точности.
Вывод:
- Как только метод завершит выполнение, наилучшая вершина симплекса будет приближением к минимуму функции.
Пример реализации в среде Maple
Функции:
# вычисляет координаты вершин симплекса с заданным центром
# и длиной ребра
# l - длина ребра
# center - центр симплекса
# dims - размерность пространства
smplx:=proc(l,center,dims:=2);
local i,j,nvert,verts;
nvert:=dims+1;
verts:=Array(1..nvert,1..dims);
for i from 1 to nvert do
for j from 1 to dims do
if j < i-1 then
verts[i,j]:=center[j]:
elif j = i-1 then
verts[i,j]:=center[j]+evalf(sqrt(j/(2*(j+1)))*l):
else
verts[i,j]:=center[j]-evalf(1/sqrt(2*j*(j+1))*l):
end if:
end do;
end do:
return verts;
end proc:
# вычисляет значение функции в вершинах симплекса
# f - функция
# sm - массив с координатами вершин симплекса
mapsimplex:=proc(f,sm);
local n,i,fs;
n:=upperbound(sm)[1]:
fs:=Array(1..n):
for i from 1 to n do
fs(i):=f(op(convert(sm[i],list))):
end do:
return fs:
end proc:
# нахождение центра масс грани симплекса
center_of_mass:=proc(smplx,idxs):
local i,n,result:
n:=upperbound(idxs):
result:=evalf(add(smplx[i],i in idxs)/n):
return result;
end proc:
# отражение точки относительно центра грани симплекса
mirror_vert:=proc(vert,smplx,sorted,excl):
local result,cm,sr:
sr:=Array(convert(sorted,list)):
ArrayTools[Remove](sr,excl):
cm:=center_of_mass(smplx,sr):
result:=2*cm-vert:
return result;
end proc:
# ищет минимум функции используя симплексный поиск
# dims - размерность задачи
# f - функция
# start - начальная точка
# l - длина ребра симплекса
# centers - массив из центров симплексов (out)
# simplexes - массив из вершин симплексов (out)
# fcenters - массив из значений функции в центрах симплексов (out)
# fsimplexes - массив из значений функции в вершинах симплексов (out)
simplex_search:=proc(dims,f,start,l,centers,simplexes,fcenters,fsimplexes):
local step,sorted,better_found,nmirror,vert_to_mirror,mirr_vert,
mirr_center,f_mirr_vert,new_simplex,new_fsimplex:
centers(1):=start:
fcenters(1):=f(op(convert(centers[1],list))):
simplexes(1):=smplx(l,centers[-1],dims):
fsimplexes(1):=mapsimplex(f,simplexes[-1]):
step:=1:
while true do
sorted:=sort(fsimplexes[-1],`>`,output=permutation):
better_found:=false;
for nmirror from 1 to dims+1 do
vert_to_mirror:=simplexes[-1][sorted[nmirror]]:
mirr_vert:=mirror_vert(vert_to_mirror, simplexes[-1], sorted, nmirror):
mirr_center:=mirror_vert(centers[-1], simplexes[-1], sorted, nmirror):
f_mirr_vert:=f(op(convert(mirr_vert,list)));
if f_mirr_vert < fsimplexes[-1][sorted[nmirror]] then
better_found:=true;
break;
end if:
end do:
if better_found then
centers(step+1):=mirr_center:
fcenters(step+1):=f(op(convert(centers(step+1),list))):
new_simplex:=Array(simplexes[-1]):
new_simplex[sorted[nmirror]]:=mirr_vert:
simplexes(step+1):=new_simplex:
new_fsimplex:=Array(fsimplexes[-1]):
new_fsimplex[sorted[nmirror]]:=f_mirr_vert:
fsimplexes(step+1):=new_fsimplex:
step++:
else
break;
end if:
end do:
return step:
end proc:Пример использования:
with(plots):with(plottools):
dimensions:=2:
func:=(x,y)->x^2+y^2:
start:=Array([-5,6]):
l:=0.9:
centers:=Array():
simplexes:=Array():
fcenters:=Array():
fsimplexes:=Array():
steps:=simplex_search(dimensions,func,start,l,centers,simplexes,fcenters,fsimplexes):
printf("Число шагов: %d\n", steps);
printf("Точка минимума: %f\n", centers[-1]);
printf("Минимум функции: %f\n", fcenters[-1]);
display(
seq(polygon(simplexes[i]),i=1..steps)
,transparency=0.7,color=green
,curve([seq(convert(centers[i],list),i=1..steps)],color=black)
);Результат:
Редукция симплекса
Редукция регулярного симплекса - это процедура уменьшения размера симплекса в методе симплексного поиска с регулярным симплексом. Как описано выше, симплекс начинает как равносторонний многогранник с радиусом R, и после выполнения определенных шагов, его размер может уменьшаться для более точной локализации минимума функции.
После шага “Сжатие” в методе симплексного поиска, если отраженная точка оказывается хуже второй по наихудшему значению вершины симплекса, то симплекс может быть сжат (уменьшен) вокруг наилучшей вершины с целью более точной локализации минимума.
Процесс редукции симплекса включает в себя уменьшение расстояния между каждой вершиной симплекса и наилучшей вершиной. Обычно это делается путем перемещения каждой вершины симплекса в сторону наилучшей вершины на некоторое фиксированное расстояние.
Формула для редукции симплекса может выглядеть следующим образом:
Для каждой вершины симплекса \(i\) (где \(i = 1, 2, ..., n\)), пересчитайте координаты следующим образом:
\(x_i^{new} = (1 - α) \cdot x_i^{old} + α \cdot x_i^{best}\),
где \(α\) - это коэффициент редукции, обычно выбирается в пределах \((0, 1)\), и он определяет, насколько сильно уменьшить расстояние между вершиной и наилучшей вершиной. Например, при \(α = 0.5\) вершины будут перемещены на половину расстояния к наилучшей вершине.
После выполнения процедуры редукции симплекса можно продолжить выполнение других шагов метода симплексного поиска в уменьшенном симплексе с целью приблизиться к минимуму функции.
Редукция симплекса позволяет более точно локализовать минимум функции и увеличить сходимость метода симплексного поиска к оптимальному решению.
Метод симплексного поиска с регулярным симплексом является надежным методом оптимизации, который хорошо работает для разнообразных функций, включая функции с локальными минимумами.
Реаллизация в среде Maple
Для реализации метода с редукцией, нужно добавить к предыдущему примеру новую процедуру:
# ищет минимум функции используя симплексный поиск
# dims - размерность задачи
# f - функция
# start - начальная точка
# l - начальная длина ребра симплекса
# centers - массив из центров симплексов (out)
# simplexes - массив из вершин симплексов (out)
# fcenters - массив из значений функции в центрах симплексов (out)
# fsimplexes - массив из значений функции в вершинах симплексов (out)
# lmin - минимальная длина ребра симплекса
simplex_search_reduction:=proc(dims,f,start,l,centers,simplexes,fcenters,fsimplexes,minl):
local step,sorted,better_found,nmirror,vert_to_mirror,mirr_vert,
mirr_center,f_mirr_vert,new_simplex,new_fsimplex,curl:
centers(1):=start:
curl:=l:
fcenters(1):=f(op(convert(centers[1],list))):
simplexes(1):=smplx(curl,centers[-1],dims):
fsimplexes(1):=mapsimplex(f,simplexes[-1]):
step:=1:
while true do
sorted:=sort(fsimplexes[-1],`>`,output=permutation):
better_found:=false;
for nmirror from 1 to dims+1 do
vert_to_mirror:=simplexes[-1][sorted[nmirror]]:
mirr_vert:=mirror_vert(vert_to_mirror, simplexes[-1], sorted, nmirror):
mirr_center:=mirror_vert(centers[-1], simplexes[-1], sorted, nmirror):
f_mirr_vert:=f(op(convert(mirr_vert,list)));
if f_mirr_vert < fsimplexes[-1][sorted[nmirror]] then
better_found:=true;
break;
end if:
end do:
if better_found then
centers(step+1):=mirr_center:
fcenters(step+1):=f(op(convert(centers(step+1),list))):
new_simplex:=Array(simplexes[-1]):
new_simplex[sorted[nmirror]]:=mirr_vert:
simplexes(step+1):=new_simplex:
new_fsimplex:=Array(fsimplexes[-1]):
new_fsimplex[sorted[nmirror]]:=f_mirr_vert:
fsimplexes(step+1):=new_fsimplex:
step++:
else
if curl <= minl then
break;
else
step++:
centers(step):=Array(centers[-1]):
fcenters(step):=Array(fcenters[-1]):
curl:=curl*0.5:
simplexes(step):=smplx(curl,centers[-1],dims):
fsimplexes(step):=mapsimplex(f,simplexes[-1]):
next:
end if:
end if:
end do:
return step:
end proc:Пример использования:
with(plots):with(plottools):
dimensions:=2:
func:=(x,y)->x^2+y^2:
start:=Array([-5,6]):
l:=6:
minl:=0.1:
centers:=Array():
simplexes:=Array():
fcenters:=Array():
fsimplexes:=Array():
steps:=simplex_search_reduction(dimensions,func,start,l,centers,simplexes,fcenters,fsimplexes,minl):
printf("Число шагов: %d\n", steps);
printf("Точка минимума: %f\n", centers[-1]);
printf("Минимум функции: %f\n", fcenters[-1]);
display(
seq(polygon(simplexes[i],transparency=0.7,color=green),i=1..steps)
,curve([seq(convert(centers[i],list),i=1..steps)],color=blue)
);Результат:
Задание
Условие
Написать приложение, реализующее метод градиентного спуска с дроблением шага для многомерной функции.
Написать приложение, реализующее метод поиска точки минимума многомерной функции по шаблону. В качестве шаблона использовать n-мерный куб. Начальная точка в центре куба.
Написать приложение, реализующее симплексный поиск точки минимума многомерной функции (с редукцией симплекса).
Варианты заданий
| 1. | \({x} ^ {4} + {y} ^ {4} -4xy\) | 16. | \({2x} ^ {4} + {3y} ^ {2} -5xy\) |
| 2. | \({x} ^ {2} + {y} ^ {2} -2x\) | 17. | \({x} ^ {4} + {3y} ^ {2} +6x\) |
| 3. | \({e} ^ {x/10} + {x} ^ {2} + {y} ^ {2}\) | 18. | \({e} ^ {x/16} - {y} ^ {4} + {3x} ^ {2}\) |
| 4. | \({x} ^ {2} -3x+ {y} ^ {2} +3y+3\) | 19. | \(3 {y} ^ {2} -2x+ {x} ^ {4} +3y-5\) |
| 5. | \({(x-3)} ^ {2} \cdot{( y+1)} ^ {2} -5\) | 20. | \({(x+5)} ^ {2} \cdot {(y-2)} ^ {2} +7\) |
| 6. | \({((x+3)\cdot y)} ^ {2} -2\) | 21. | \({((x-5)\cdot 7y)} ^ {2} -3\) |
| 7. | \({x} ^ {2} + {y} ^ {4} +3xy-5\) | 22. | \({(x-7)} ^ {2} \cdot {(y-2)} ^ {2} +1\) |
| 8. | \({x} ^ {2} + {y} ^ {2} -5y\) | 23. | \({((x+3)\cdot y)} ^ {2} -2\) |
| 9. | \({e} ^ {y/11} + {x} ^ {4} + {y} ^ {2}\) | 24. | \(6 {x} ^ {2} + {y} ^ {4} +2xy\) |
| 10. | \({x} ^ {4} -3y+ {y} ^ {2} +2x-7\) | 25. | \({x} ^ {4} + {4y} ^ {2} -5x\) |
| 11. | \({(x-1)} ^ {2} \cdot{(y+3)} ^ {2} -1\) | 26. | \({e} ^ {y/15} + {x} ^ {4} + {3y} ^ {2}\) |
| 12. | \({((y+1)\cdot x)} ^ {2} +4\) | 27. | \({2x} ^ {2} +x+ {y} ^ {4} -7y+10\) |
| 13. | \({((y+3)\cdot x)} ^ {2} +1\) | 28. | \({(x-1)} ^ {2} \cdot{(y-4)} ^ {2} -3\) |
| 14. | \({x} ^ {4} + {y} ^ {4} +2xy-20\) | 29. | \({((x+1)\cdot 2y)} ^ {2} -10\) |
| 15. | \({x} ^ {4} + {y} ^ {2} -8x\) | 30. | \({5x} ^ {2} +y+ {4y} ^ {4} -7x+2\) |