Лаб. работа “Haskell”

Разработка и оптимизация интеллектуальных информационных систем

Функциональное программирование

Практика

Автор

Бизюк Андрей

Дата публикации

11 февраля 2025 г.

Установка среды разработки для Haskell

Для установки компилятора GHC в ОС Windows есть несколько возможностей:

Установка через GHCup
Установка через Chocolatey в привилегированном режиме
Установка через Chocolatey в непривилегированном режиме
Установка в среде WSL

Установка через GHCup

GHCup – это основной инсталлятор для различных компонентов среды разработки Haskell. С помощью него можно устанавливать, обновлять и переключать версии компилятора GHC, менеджеров проектов Cabal и Stack, языковой сервер HLS.

Основное расширение поддержки Haskell в VSCode требует наличия установленного GHCup.

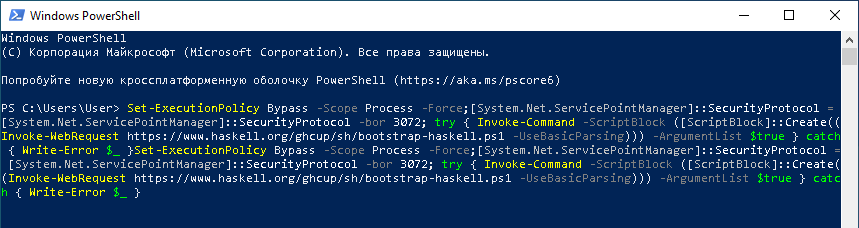
Для установки GHCup в Windows 10 или windows 11, нужно открыть PowerShell и вставить следующую команду:

Set-ExecutionPolicy Bypass -Scope Process -Force;[System.Net.ServicePointManager]::SecurityProtocol = [System.Net.ServicePointManager]::SecurityProtocol -bor 3072; try { Invoke-Command -ScriptBlock ([ScriptBlock]::Create((Invoke-WebRequest https://www.haskell.org/ghcup/sh/bootstrap-haskell.ps1 -UseBasicParsing))) -ArgumentList $true } catch { Write-Error $_ }

На вопросы скрипта можно просто нажимать Enter, принимая ответы по умолчанию.

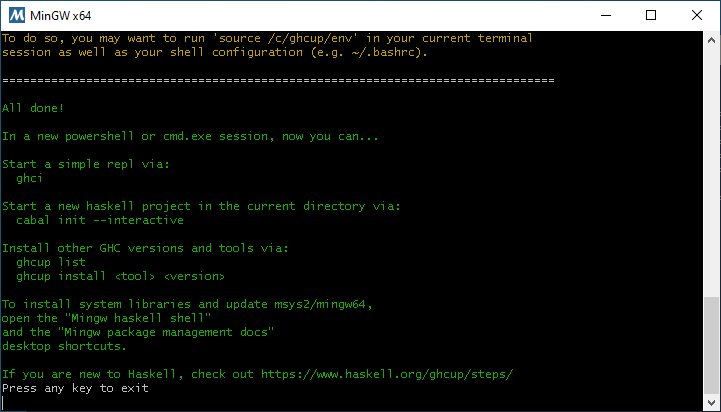
После окончания установки нужно нажать Enter:

На рабочем столе появятся ярлыки:

При необходимости удаления установленных приложений, нужно воспользоваться ярлыком “Uninstall Haskell”.

Теперь можно установить расширение VSCode для поддержки Haskell:

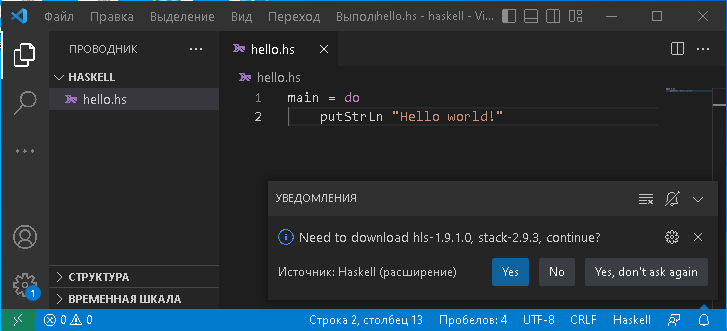
При первом открытии файла *.hs, расширение попросит установить недостающие компоненты, нужно согласиться.

После установки компонентов, можно работать с Haskell в VSCode с поддержкой автодополнения и проверки синтаксиса.

Установка через Chocolatey в привилегированном режиме

Предпочтительным способом установки программного обеспечения в ОС Windows 10 или Windows 11 является использование менеджеров пакетов WinGet или Chocolatey. Обычно, установка программного обеспечения требует повышенных привилегий, однако некоторое программное обеспечение можно установить в непривилегированном режиме.

Для установки компилятора Haskell, необходимо сначала установить менеджер пакетов Chocolatey. Наиболее актуальные инструкции по установке Chocolatey находятся на сайте проекта: https://docs.chocolatey.org/en-us/choco/setup

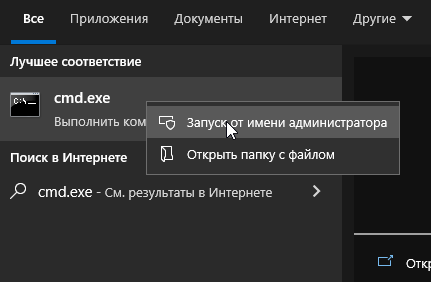
Для установки требуется сначала запустить командную оболочку cmd.exe либо powershell.exe с правами администратора. Для этого, сначала, нужно открыть меню Пуск и набрать для поиска “cmd.exe” (или “powershell.exe”). Далее требуется кликнуть правой клавишей мыши на результате поиска и выбрать “Запуск от имени администратора”.

Рисунок 1 - запуск оболочки с правами администратора

После запуска командной оболочки, нужно вставить и выполнить соответствующие команды:

для “cmd.exe”:

@"%SystemRoot%\System32\WindowsPowerShell\v1.0\powershell.exe" -NoProfile -InputFormat None -ExecutionPolicy Bypass -Command "[System.Net.ServicePointManager]::SecurityProtocol = 3072; iex ((New-Object System.Net.WebClient).DownloadString( 'https://community.chocolatey.org/install.ps1'))" && SET "PATH=%PATH%;%ALLUSERSPROFILE%\chocolatey\bin"

для “powershell.exe”:

Сначала выполняем команду:

Set-ExecutionPolicy Bypass -Scope Process

Затем выполняем:

Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol = [System.Net.ServicePointManager]::SecurityProtocol -bor 3072; iex ((New-Object System.Net.WebClient).DownloadString( 'https://community.chocolatey.org/install.ps1'))

После успешной установки Chocolatey можно установить компилятор Haskell. Для этого нужно выполнить в командной оболочке команду:

choco install ghc -y

Установка через Chocolatey в непривилегированном режиме

Для установки менеджера пакетов Chocolatey в случае отсутсвия прав администратора, требуется выполнить следующие действия:

Создать файл `ChocolateyInstallNonAdmin.ps1` со следующим содержимым:

ChocolateyInstallNonAdmin.ps1

# Set directory for installation - Chocolatey does not lock
# down the directory if not the default
$InstallDir='C:\ProgramData\chocoportable'
$env:ChocolateyInstall="$InstallDir"

# If your PowerShell Execution policy is restrictive, you may
# not be able to get around that. Try setting your session to
# Bypass.
Set-ExecutionPolicy Bypass -Scope Process -Force;

# All install options - offline, proxy, etc at
# https://chocolatey.org/install
iex ((New-Object System.Net.WebClient).DownloadString( 'https://community.chocolatey.org/install.ps1'))

Совет

Для этого может потребоваться включение показа расширений файлов в проводнике Windows:

Вид / Параметры / Изменить параметры папок и поиска / Вид

Затем нужно снять галочку “Скрывать расширения для зарегистрированных типов файлов”

Открыть командную оболочку `powershell.exe` в том же каталоге, где сохранен скрипт из предыдущего пункта.

Выполнить в оболочке следующую команду:

Set-ExecutionPolicy Bypass -Scope Process -Force;

Запустить `.\ChocolateyInstallNonAdmin.ps1`

choco install ghc -y

Работа с Haskell в VSCode

Установка расширения

Для более удобной работы с кодом на Haskell в среде разработки VSCode, можно установить специальное расширение:

Создание файла исходного кода

Для того, чтобы создать файл исходного кода программы на языке Haskell в VSCode, нужно сначала выбрать рабочую папку проекта:

После выбора рабочей папки можно создать файл исходного кода:

Рисунок 3 - создание файла исходного кода

Файлы исходного кода на языке Haskell имеют расширение .hs

Компиляция и запуск программы

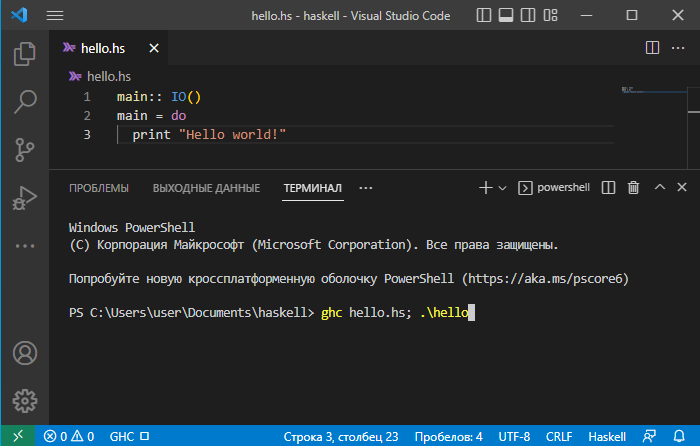
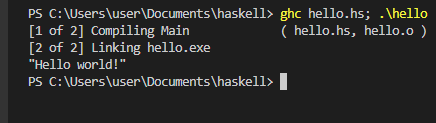
После написания кода программы, нужно ее откомпилировать и запустить. Для этого сначала нужно открыть терминал сочетанием клавиш Ctrl+` . В терминале нужно ввести команду

ghc hello.hs; .\hello

где вместо “hello” нужно подставить название файла с исходным кодом.

Пример простейшей программы на языке Haskell:

main:: IO()
main = do
  print "Hello world!"

Рисунок 5 - результат компиляции и запуска программы

Типы и функции в Haskell

Типы

Программы на языке Haskell представляют собой выражения, вычисление которых приводит к значениям. Каждое значение имеет тип. Интуитивно тип можно понимать просто как множество допустимых значений выражения. Для того, чтобы узнать тип некоторого выражения, можно использовать команду интерпретатора :type (или :t). Кроме того, можно выполнить команду :set +t, для того, чтобы интерпретатор автоматически печатал тип каждого вычисленного результата.

Основными типами языка Haskell являются:

Типы Integer и Int используется для представления целых чисел, причем значения типа Integer не ограничены по длине; тип Int представляет целые числа фиксированной длины.
Типы Float и Double используется для представления вещественных чисел.
Тип Bool содержит два значения: True и False, и предназначен для представления результата логических выражений.
Тип Char используется для представления символов.

Имена типов в языке Haskell всегда начинаются с заглавной буквы.

Язык Haskell является сильно типизированным языком программирования. Тем не менее в большинстве случаев программист не обязан объявлять, каким типам принадлежат вводимые им переменные. Интерпретатор сам способен вывести типы употребляемых пользователем переменных. Однако, если все же для каких-либо целей необходимо объявить, что некоторое значение принадлежит некоторому типу, используется конструкция вида: переменная::Тип. Если включена опция интерпретатора +t, он печатает значения в таком же формате.

Развитая система типов и строгая типизация делают программы на языке Haskell безопасными по типам. Гарантируется, что в правильной программе на языке Haskell все типы используются правильно. С практической точки зрения это означает, что программа на языке Haskell при выполнении не может вызвать ошибок доступа к памяти (Access violation). Также гарантируется, что в программе не может произойти использование неинициализированных переменных. Таким образом, многие ошибки в программе отслеживаются на этапе ее компиляции, а не выполнения.

Кортежи

Помимо перечисленных выше простых типов, в языке Haskell можно определять значения составных типов. Например, для задания точки на плоскости необходимы два числа, соответствующие ее координатам.

В языке Haskell пару можно задать, перечислив компоненты через запятую и взяв их в скобки: (5,3). Компоненты пары не обязательно должны принадлежать одному типу: можно составить пару, первым элементом которой будет строка, а вторым - число и т.д. В общем случае, если a и b – некоторые произвольные типы языка Haskell, тип пары, в которой первый элемент принадлежит типу a, а второй - типу b, обозначается как (a,b). Например, пара (5,3) имеет тип (Integer, Integer); пара (1, 'a') принадлежит типу (Integer, Char).

Можно привести и более сложный пример: пара ((1,'a'),1.2) принадлежит типу ((Integer,Char),Double).

Следует обратить внимание, что хотя конструкции вида (1,2) и (Integer,Integer) выглядят похоже, в языке Haskell они обозначают совершенно разные сущности. Первая является значением, в то время как последняя - типом.

Для работы с парами в языке Haskell существуют стандартные функции fst и snd, возвращающие, соответственно, первый и второй элементы пары (названия этих функций происходят от английских слов first(первый) и second (второй)). Таким образом, их можно использовать следующим образом:

Prelude>fst (5, True)
5 :: Integer
Prelude>snd (5, True)
True :: Bool

Кроме пар, аналогичным образом можно определять тройки, четверки и т.д. Их типы записываются аналогичным образом.

Prelude>(1,2,3)
(1,2,3) :: (Integer,Integer,Integer)
Prelude>(1,2,3,4)
(1,2,3,4) :: (Integer,Integer,Integer,Integer)

Такая структура данных называется кортежем. В кортеже может храниться фиксированное количество разнородных данных. Функции fst и snd определены только для пар и не работают для других кортежей. При попытке использовать их, например, для троек, интерпретатор выдает сообщение об ошибке.

Элементом кортежа может быть значение любого типа, в том числе и другой кортеж. Для доступа к элементам кортежей, составленных из пар, может использоваться комбинация функций fst и snd. Следующий пример демонстрирует извлечение элемента ‘a’ из кортежа (1, ('a', 23.12)):

Prelude>
fst (snd (1, ('a', 23.12)))
'a' :: Char

Списки

В отличие от кортежей, список может хранить произвольное количество элементов. Чтобы задать список в Haskell, необходимо в квадратных скобках перечислить его элементы через запятую. Все эти элементы должны принадлежать одному и тому же типу. Тип списка с элементами, принадлежащими типу a, обозначается как [a].

Prelude>[1,2]
[1,2] :: [Integer]
Prelude>['1','2','3']
['1','2','3'] :: [Char]

В списке может не быть ни одного элемента. Пустой список обозначается как []. Оператор : (двоеточие) используется для добавления элемента в начало списка. Его левым аргументом должен быть элемент, а правым - список:

Prelude>1:[2,3]
[1,2,3] :: [Integer]
Prelude>'5':['1','2','3','4','5']
['5','1','2','3','4','5'] :: [Char]
Prelude>False:[]
[False] :: [Bool]

С помощью оператора (:) и пустого списка можно построить любой список:

Prelude>1:(2:(3:[]))
[1,2,3] :: Integer

Оператор (:) ассоциативен вправо, поэтому в приведенном выше выражении можно опустить скобки:

Prelude>1:2:3:[]
[1,2,3] :: Integer

Элементами списка могут быть любые значения – числа, символы, кортежи, другие списки и т.д.

Prelude>[(1,'a'),(2,'b')]
[(1,'a'),(2,'b')] :: [(Integer,Char)]
Prelude>[[1,2],[3,4,5]]
[[1,2],[3,4,5]] :: [[Integer]]

Для работы со списками в языке Haskell существует большое количество функций. В данной лабораторной работе рассмотрим только некоторые из них.

Функция head возвращает первый элемент списка.
Функция last возвращает последний элемент списка.
Функция tail возвращает список без первого элемента
Функция init возвращает список без последнего элемента
Функция null проверяет список на пустоту. Если в качестве аргумента этой операции будет задан пустой список, то функция выдаст значение True, в противном случае – False
Функция length возвращает длину списка.
Функция elem проверяет наличие элемента в списке.
Функция take возвращает список, состоящий из n первых элементов исходного списка.
Функция zip возвращает список, состоящий из пар объединенных исходных списков.
Функция !! возвращает элемент, номер которого задан (начиная с 0).

Функции head и tail определены для непустых списков. При попытке применить их к пустому списку интерпретатор сообщает об ошибке. Примеры работы с указанными функциями:

Prelude>head [1,2,3]
1 :: Integer
Prelude>tail [1,2,3]
[2,3] :: [Integer]
Prelude>tail [1]
[] :: Integer
Prelude>length [1,2,3]
3 :: Int
Prelude> elem 2 [1,2,3]
True :: Bool
Prelude> take 2 [1,2,3]
[1,2] :: [Integer]
Prelude> zip ["20","30"] [1,2,3]
[("20",1),("30",2)] :: [([Char],Integer)]
Prelude> [1,2,3,4,5] !! 3
4 :: Integer

Заметьте, что результат функции length принадлежит типу Int, а не типу Integer. Для соединения (конкатенации) списков в Haskell определен оператор ++.

Prelude>[1,2]++[3,4]
[1,2,3,4] :: Integer

Строки

Строковые значения в языке Haskell, как и в Си, задаются в двойных кавычках. Они принадлежат типу String.

Prelude>"hello"
"hello" :: String

В действительности строки являются списками символов; таким образом, выражения "hello", ['h','e','l','l','o'] и 'h':'e':'l':'l':'o':[] означают одно и то же, а тип String является синонимом для [Char]. Все функции для работы со списками можно использовать при работе со строками:

Prelude>head "hello"
'h' :: Char
Prelude>tail "hello"
"ello" :: [Char]
Prelude>length "hello"
5 :: Int
Prelude>"hello" ++ ", world"
"hello, world" :: [Char]

Для преобразования числовых значений в строки и наоборот существуют функции read и show:

Prelude>show 1
"1" :: [Char]
Prelude>"Formula " ++ show 1
"Formula 1" :: [Char]
Prelude>1 + read "12"
13 :: Integer

Если функция read не сможет преобразовать строку в число, она сообщит об ошибке.

Функции

Теперь можно перейти к определению функций.

square :: Integer -> Integer
square x = x * x

Первая строка (square :: Integer -> Integer) объявляет, что мы определяем функцию square, принимающую параметр типа Integer и возвращающую результат типа Integer.

Вторая строка (square x = x * x) является непосредственно определением функции. Функция square принимает один аргумент и возвращает его квадрат.

Функции в языке Haskell являются значениями “первого класса”. Это означает, что они “равноправны” с такими значениями, как целые и вещественные числа, символы, строки, списки и т.д. Функции можно передавать в качестве аргументов в другие функции, возвращать их из функций и т.п. Как и все значения в языке Haskell, функции имеют тип. Тип функции, принимающей значения типа a и возвращающей значения типа b обозначается как a->b

Заметим, что в принципе объявление типа функции square не являлось необходимым: интерпретатор сам мог вывести необходимую информацию о типе функции из ее определения. Однако, во-первых, выведенный тип был бы более общим, чем Integer -> Integer, а во-вторых, явное указание типа функции является “хорошим тоном” при программировании на языке Haskell, поскольку объявление типа служит своего рода документацией к функции и помогает выявлять ошибки программирования. Имена определяемых пользователем функций и переменных должны начинаться с латинской буквы в нижнем регистре. Остальные символы в имени могут быть прописными или строчными латинскими буквами, цифрами или символами _ и ' (подчеркивание и апостроф). Таким образом, ниже перечислены примеры правильных имен переменных:

var
var1
variableName
variable_name
var'

Условные выражения

В определении функции в языке Haskell можно использовать условные выражения. Запишем функцию signum, вычисляющую знак переданного ей аргумента:

signum :: Integer -> Integer
signum x = if x > 0 then 1
else if x < 0 then -1
else 0

Условное выражение записывается в виде: if условие then выражение else выражение.

Обратите внимание, что хотя по виду это выражение напоминает соответствующий оператор в языке Си или Паскаль, в условном выражении языка Haskell должны присутствовать и then-часть и else-часть. Выражения в then-части и в else-части условного оператора должны принадлежать одному типу.

Условие в определении условного оператора представляет собой любое выражение типа Bool. Примером таких выражений могут служить сравнения. При сравнении можно использовать следующие операторы:

<, >, <=, >= – эти операторы имеют такой же смысл, как и в языке Си (меньше, больше, меньше или равно, больше или равно).
== – оператор проверки на равенство.
/= – оператор проверки на неравенство.

Выражения типа Bool можно комбинировать с помощью общепринятых логических операторов && и || (И и ИЛИ), и функции отрицания not. Примеры допустимых условий:

x >= 0 && x <= 10
x > 3 && x /= 10
(x > 10 || x < -10) && not (x == y)

Разумеется, можно определять свои функции, возвращающие значения типа Bool, и использовать их в качестве условий. Например, можно определить функцию isPositive, возвращающую True, если ее аргумент неотрицателен и False в противном случае:

isPositive :: Integer -> Bool
isPositive x = if x > 0 then True else False

Теперь функцию signum можно определить следующим образом:

signum :: Integer -> Integer
signum x = if isPositive x then 1
           else if x < 0 then -1
                else 0

Отметим, что функцию isPositive можно определить и проще:

isPositive x = x > 0

Функции многих переменных и порядок определения функций

До сих пор мы определяли функции, принимающие один аргумент. Разумеется, в языке Haskell можно определять функции, принимающие произвольное количество аргументов. Определение функции add, принимающей два целых числа и возвращающей их сумму, выглядит следующим образом:

add :: Integer -> Integer -> Integer
add x y = x + y

Тип функции add может выглядеть несколько загадочно. В языке Haskell считается, что операция -> ассоциативна вправо. Таким образом, тип функции add может быть прочитан как Integer -> (Integer -> Integer), т.е. в соответствии с правилом каррирования, результатом применения функции add к одному аргументу будет функция, принимающая один параметр типа Integer. Вообще, тип функции, принимающей n аргументов, принадлежащих типам t1, t2,..., tn, и возвращающей результат типа a, записывается в виде t1->t2->...->tn->a.

Следует сделать еще одно замечание, касающееся порядка определения функций. В предыдущем разделе мы определили две функции, signum и isPositive, одна из которых использовала для своего определения другую. Возникает вопрос: какая из этих функций должна быть определена раньше? Напрашивается ответ, что определение isPositive должно предшествовать определению функции signum; однако в действительности в языке Haskell порядок определения функций не имеет значения! Таким образом, функция isPositive может быть определена как до, так и после функции signum.

Функции высшего порядка

Рассмотрим две задачи. Пусть задан список чисел. Необходимо написать две функции, первая из которых возвращает список квадратных корней этих чисел, а вторая – список их логарифмов. Эти функции можно определить так:

sqrtList [] = []
sqrtList (x:xs) = sqrt x : sqrtList xs
logList [] = []
logList (x:xs) = log x : logList xs

Можно заметить, что эти функции используют один и тот же подход, и все различие между ними заключается в том, что в одной из них для вычисления элемента нового списка используется функция квадратного корня, а в другой – логарифм. Можно ли абстрагироваться от конкретной функции преобразования элемента? Оказывается, можно. Вспомним, что в Haskell функции являются элементами «первого класса»: их можно передавать в другие функции в качестве параметров. Определим функцию transformList, которая принимает два параметра: функцию преобразования и преобразуемый список.

transformList f [] = []
transformList f (x:xs) = f x : transformList f xs

Теперь функции sqrtList и logList можно определить так:

sqrtList l = transformList sqrt l
logList l = transformList log l

Или, с учетом каррирования:

sqrtList = transformList sqrt
logList = transformList log

Функция map

В действительности функция, полностью аналогичная transformList ,уже определена в стандартной библиотеке языка и называется map (от англ. map – отображение). Она имеет следующий тип:

map :: (a -> b) -> [a] -> [b]

Это означает, что ее первым аргументом является функция типа a->b ,отображающая значения произвольного типа a в значения типа b (вообще говоря, эти типы могут совпадать). Вторым аргументом функции является список значений типа a. Тогда результатом функции будет список значений типа b.

Функции, подобные map , принимающие в качестве аргументов другие функции, называются функциями высшего порядка. Их очень широко используют при написании функциональных программ. С их помощью можно явно отделить частные детали реализации алгоритма (например, конкретную функцию преобразования в map) от его высокоуровневой структуры (поэлементное преобразование списка). Алгоритмы, представленные с использованием функций высшего порядка, как правило, более компактны и наглядны, чем реализации, ориентированные на конкретные частности.

Функция filter

Следующим примером широко используемой функции высшего порядка является функция filter. По заданному предикату (функции, возвращающей булевское значение) и списку она возвращает список тех элементов, которые удовлетворяют заданному предикату:

filter :: (a -> Bool) -> [a] -> [a]
filter p [] = []
filter p (x:xs) | p x = x : filter xs
                | otherwise = filter xs

Например, функция, получающая из списка чисел его положительные элементы, определяется так:

getPositive = filter isPositive
isPositive x = x > 0

Функции foldr и foldl

Более сложным примером являются функции foldr и foldl. Рассмотрим функции, возвращающие сумму и произведение элементов списка:

sumList [] = 0
sumList (x:xs) = x + sumList xs
multList [] = 1
multList (x:xs) = x * multList xs

Здесь также можно увидеть общие элементы: начальное значение (0 для суммирования, 1 для умножения) и функция, комбинирующая значения между собой. Функция foldr является очевидным обобщением такой схемы:

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)

Функция foldr принимает в качестве первого аргумента комбинирующую функцию (заметим, что она может принимать аргументы разных типов, но тип результата должен совпадать с типом второго аргумента). Вторым аргументом функции foldr является начальное значение для комбинирования. Третьим аргументом передается список. Функция осуществляет «свертку» списка в соответствие с переданными параметрами. Для того, чтобы лучше понять, как работает функция foldr , запишем ее определение с использованием инфиксной нотации:

foldr f z [] = z
foldr f z (x:xs) = x `f` (foldr f z xs)

Представим список элементов [a,b,c,…,z] с использованием оператора :. Правило применения функции foldr таково: все операторы : заменяются на применение функции f в инфиксном виде (f), а символ пустого списка [] заменяется на начальное значение комбинирования. Шаги преобразования можно изобразить так (предполагаем, что начальное значение равно init )

[a,b,c,...,z]
a : b : c : ... z : []
a : (b : (c : (... (z : []))))
a `f` (b `f` (c `f` (... (z `f` init)...)))

С помощью функции foldr функции суммирования и умножения элементов списка определяется так:

sumList = foldr (+) 0
multList = foldr (*) 1

Рассмотрим, как вычисляются значения этих функций на примере списка [1,2,3] :

[1,2,3]
1 : 2 : 3 : []
1 : (2 : (3 : []))
1 + (2 + (3 + 0))

Аналогично для умножения:

[1,2,3]
1 : 2 : 3 : []
1 : (2 : (3 : []))
1 * (2 * (3 * 1))

Название функции происходит от английского слова fold – сгибать, складывать (например, лист бумаги). Буква r в названии функции происходит от слова right (правый) и показывает ассоциативность применяемой для свертки функции. Так, из приведенных примеров видно, что применение функции группируется вправо. Определение функции foldl, где l указывает на то, что применение операции группируется влево, приведено ниже:

foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs

Шаги преобразования можно изобразить аналогично:

[a,b,c,...,z]
[]:a : b : c : ... : z
((([]: a) : b) : c) : ... : z
(((init `f` a) `f` b) `f` c) `f` ... `f` z

Для ассоциативных операций, таких как сложение и умножение, функции foldr и foldl эквивалентны, однако если операция не ассоциативна, их результат будет отличаться:

Main>foldr (-) 0 [1,2,3]
2
Main>foldl (-) 0 [1,2,3]
-6

Действительно, в первом случае вычисляется величина 1 - (2 - (3 - 0)) = 2, а во– величина ((0 - 1) - 2) - 3 = -6.

Другие функции высшего порядка

В стандартной библиотеке определена функция zip . Она преобразует два списка в список пар:

zip :: [a] -> [b] -> [(a,b)]
zip (a:as) (b:bs) = (a,b):zip as bs
zip _ _ = []

Пример применения:

Prelude>zip [1,2,3] ['a','b','c']
[(1,'a'),(2,'b'),(3,'c')]
Prelude>zip [1,2,3] ['a','b','c','d']
[(1,'a'),(2,'b'),(3,'c')]

Заметьте, что длина результирующего списка равна длине самого короткого исходного списка. Обобщением этой функции является функция высшего порядка zipWith, «соединяющая» два списка с помощью указанной функции:

zipWith :: (a->b->c) -> [a]->[b]->[c]
zipWith z (a:as) (b:bs) = z a b : zipWith z as bs
zipWith _ _ _ = []

С помощью этой функции легко определить, например, функцию поэлементного суммирования двух списков:

sumList xs ys = zipWith (+) xs ys

или, с учетом каррирования:

sumList = zipWith (+)

Лямбда-абстракции

При использовании функций высшего порядка зачастую необходимо определять много небольших функций. С ростом объема программы необходимость придумывать имена для вспомогательных функций все больше мешает. Однако в языке Haskell, как и в лежащем в его основе лямбда-исчислении, можно определять безымянные функции с помощью конструкции лямбда-абстракции. Например, безымянные функции, возводящая свой аргумент в квадрат, прибавляющие единицу и умножающие на два, записывается следующим образом:

\x -> x * x
\x -> x + 1
\x -> 2 * x

Их теперь можно использовать в аргументах функций высших порядков. Например, функцию для возведения элементов списка в квадрат можно записать так:

squareList l = map (\x -> x * x) l

Функция getPositive может быть определена следующим образом:

--Функции для получения положительных элементов списка
getPositive = filter (\x -> x> 0)

Можно определять лямбда-абстракции для нескольких переменных:

\x y -> 2 * x + y

Лямбда-абстракции можно использовать наравне с обычными функциями, например, применять к аргументам:

Main>(\x -> x + 1) 2
3
Main>(\x -> x * x) 5
25
Main>(\x -> 2 * x + y) 1 2
4

С помощью лямбда-абстракций можно определять функции. Например, запись

square = \x -> x * x

полностью эквивалентна

square x = x * x

Секции

Функции можно применять частично, т.е. не задавать значение всех аргументов. Например, если функция add определена как

add x y = x + y

то можно определить функцию inc, увеличивающую свой аргумент на 1 следующим образом:

inc = add 1

Оказывается, бинарные операторы, как встроенные в язык, так и определенные пользователям, также можно применять лишь к части своих аргументов (поскольку количество аргументов у бинарных операторов равно двум, эта часть состоит из одного аргумента). Бинарная операция, примененная к одному аргументу, называется секцией . Пример:

(x+) = \y -> x+y
(+y) = \x -> x+y
(+) = \x y -> x+y

Скобки здесь обязательны. Таким образом, функции add и inc можно определить так:

add = (+)
inc = (+1)

Секции особенно полезны при использовании их в качестве аргументов функций высшего порядка. Вспомним определение функции для получения положительных элементов списка:

getPositive = filter (\x -> x > 0)

С использованием секций она записывается более компактно:

getPositive = filter (>0)

Функция для удвоения элементов списка:

doubleList = map (*2)

Лаб. работа №1 - Установка и настройка среды разработки

Ознакомьтесь с разделами Установка среды разработки для Haskell и Работа с Haskell в VSCode.
Установите компилятор Haskell на свой компьютер. Если вы работаете в лаборатории университета, нужно использовать инструкции из пункта “Установка в непривилегированном режиме”.
Установите расширение “Haskell” или “Simple GHC (Haskell) Integration” для VSCode.
Создайте каталог проекта и файл исходного кода. Напишите код простейшей программы, которая выводит на экран ваше имя и группу.
Откомпилируете и запустите программу. Убедитесь, что программа выполнилась успешно. Исправьте ошибки, если они возникают.

Лаб. работа №2 - Типы и функции

Цель работы

Приобрести навыки написания программ на языке Haskell. Получить представление об основных типах языка Haskell. Научиться определять простейшие функции.

Самостоятельные задания:

Изучите теоретический материал в разделе Типы и функции в Haskell.
Напишите функции, решающие следующие задачи:

Три точки A, B, C лежат на одной прямой. Заданы длины AB, BC, AC. Может ли точка A лежать между точками B и C.
Чему равен угол, если два смежных с ним угла составляют в сумме заданное число градусов.
Периметр равнобедренного треугольника равен P метрам, а боковая сторона L. Найти основание треугольника.
Найти углы треугольника, еcли они пропорциональны заданным числам A, B, C.
В равнобедренном треугольнике боковая сторона A, а основание B. Найти высоту, опущенную на основание.
Даны координаты центров и радиусы двух окружностей на плоскости. Может ли вторая окружность целиком содержится внутри первой? Если нет, то сколько точек пересечения имеют окружности?
Можно ли из отрезков с заданными длинами A, B, C построить прямоугольный треугольник?
Можно ли из круглого листа железа диаметром D метров вырезать квадрат со стороной A метров?
Стороны треугольника A, B, C. Найти высоту, опущенную на строну C.
Высота равнобедренного треугольника H метров, основание L. Найти углы треугольника и длину боковой стороны.
По данной хорде A найти длину дуги, если она соответствует центральному углу в C градусов.
Найти точку, равноудаленную от осей координат и от точки с заданными координатами (x,y).
Даны четыре точки A, B, C, D на плоскости. Является ли четырехугольник ABCD параллелограммом?
Составить уравнение прямой, проходящей через 2 заданные точки.
Даны четыре точки A, B, C, D на плоскости. Является ли четырехугольник ABCD квадратом?

Лаб. работа №3 – функции высших порядков

Цель работы

Получить представление о функциях высших порядков в языке Haskell. Научиться использовать функции высших порядков.

Самостоятельные задания:

Изучите теоретический материал в разделе Функции высших порядков.
Определите следующие функции с использованием функций высшего порядка:

Функция вычисления геометрического среднего элементов списка вещественных чисел с использованием функции foldr. Функция должна осуществлять только один проход по списку.
Функция, вычисляющая скалярное произведение двух списков (используйте функции foldr и zipWith).
Функция countNegat, возвращающая количество отрицательных элементов в списке.
Функция quicksort, осуществляющая быструю сортировку списка по следующему рекурсивному алгоритму. Для того, чтобы отсортировать список xs, из него выбирается первый элемент (обозначим его x). Остальной список делится на две части: список, состоящий из элементов xs, меньших x и список элементов, больших x. Эти списки сортируются (здесь проявляется рекурсия, поскольку они сортируются этим же алгоритмов), а затем из них составляется результирующий список вида as ++ [x] ++ bs, где as и bs — отсортированные списки меньших и больших элементов соответственно.
Определенная в предыдущем пункте функция quicksort сортирует список в порядке возрастания. Обобщите ее: пусть она принимает еще один — функцию сравнения типа a -> a -> Bool и сортирует список в соответствие с нею.

Лаб. работа №4 – Рекурсия

Цель работы

Закрепить понимание рекурсии, а также научиться применять её для решения различных задач.

Самостоятельные задания:

Факториал: Напишите рекурсивную функцию для вычисления факториала числа. Убедитесь, что функция корректно обрабатывает случай для 0.
Числа Фибоначчи: Реализуйте функцию, которая возвращает n-ое число Фибоначчи с использованием рекурсии.
Сумма списка: Напишите рекурсивную функцию, которая вычисляет сумму элементов списка.
Длина списка: Реализуйте функцию, которая возвращает длину списка, используя рекурсию.
Реверс списка: Напишите рекурсивную функцию, которая возвращает список в обратном порядке.
Проверка на палиндром: Реализуйте функцию, которая проверяет, является ли список палиндромом (читается одинаково с начала и с конца).
Поиск элемента в списке: Напишите рекурсивную функцию, которая проверяет, содержится ли элемент в списке.
Удаление элемента из списка: Реализуйте функцию, которая удаляет все вхождения элемента из списка.
Подсчёт количества вхождений элемента: Напишите функцию, которая считает, сколько раз элемент встречается в списке.
Функция take: Реализуйте свою версию функции take, которая возвращает первые n элементов списка.
Быстрая сортировка (quicksort): Реализуйте алгоритм быстрой сортировки с использованием рекурсии.
Функция zip: Напишите свою версию функции zip, которая объединяет два списка в список кортежей.
Функция flatten: Реализуйте функцию, которая “разворачивает” список списков в один список.
Генерация всех подмножеств: Напишите функцию, которая возвращает все подмножества списка.
Поиск наибольшего элемента: Реализуйте функцию, которая находит наибольший элемент в списке.
Функция dropWhile: Реализуйте свою версию функции dropWhile, которая удаляет элементы из начала списка, пока они удовлетворяют условию.
Функция group: Напишите функцию, которая группирует одинаковые элементы списка в подсписки.
Функция tails: Реализуйте функцию, которая возвращает все суффиксы списка.
Функция inits: Напишите функцию, которая возвращает все префиксы списка.
Функция permutations: Реализуйте функцию, которая возвращает все перестановки списка.

Лаб. работа №5 – Паттерн-матчинг

Паттерн-матчинг (pattern matching) — это мощный инструмент в Haskell, который позволяет декомпозировать данные и сопоставлять их с определёнными шаблонами.

Цель работы

Закрепить понимание паттерн-матчинга.

Самостоятельные задания:

Факториал с паттерн-матчингом: Реализуйте функцию вычисления факториала, используя паттерн-матчинг для обработки базового случая.
Числа Фибоначчи: Напишите функцию для вычисления n-го числа Фибоначчи, используя паттерн-матчинг для базовых случаев.
Сумма списка: Реализуйте функцию, которая вычисляет сумму элементов списка, используя паттерн-матчинг для обработки пустого списка и списка с головой и хвостом.
Длина списка: Напишите функцию, которая возвращает длину списка, используя паттерн-матчинг.
Реверс списка: Реализуйте функцию, которая возвращает список в обратном порядке, используя паттерн-матчинг.
Проверка на пустой список: Напишите функцию, которая проверяет, является ли список пустым, используя паттерн-матчинг.
Первый элемент списка: Реализуйте функцию, которая возвращает первый элемент списка, используя паттерн-матчинг. Если список пуст, верните Nothing.
Последний элемент списка: Напишите функцию, которая возвращает последний элемент списка, используя паттерн-матчинг.
Удаление первого элемента: Реализуйте функцию, которая удаляет первый элемент списка, используя паттерн-матчинг.
Проверка на палиндром: Напишите функцию, которая проверяет, является ли список палиндромом, используя паттерн-матчинг.
Сопоставление с кортежами: Напишите функцию, которая принимает кортеж из двух элементов и возвращает их сумму.
Сопоставление с пользовательскими типами данных: Создайте тип данных Shape, который может быть кругом (Circle) или прямоугольником (Rectangle). Напишите функцию, которая вычисляет площадь фигуры.
```
data Shape = Circle Float | Rectangle Float Float
```
Сопоставление с вложенными структурами: Создайте тип данных Tree, представляющий бинарное дерево. Напишите функцию, которая вычисляет глубину дерева.
```
data Tree a = Empty | Node (Tree a) a (Tree a)
```
Сопоставление с Maybe: Напишите функцию, которая принимает Maybe Int и возвращает 0, если значение Nothing, иначе возвращает значение.
Сопоставление с Either: Реализуйте функцию, которая принимает Either String Int и возвращает строку, если значение Left, или число, если значение Right.
Сопоставление с ассоциативными списками: Напишите функцию, которая ищет значение по ключу в ассоциативном списке (списке пар).
Сопоставление с числами: Напишите функцию, которая классифицирует число как отрицательное, ноль или положительное.
Сопоставление с символами: Реализуйте функцию, которая проверяет, является ли символ гласной буквой.
Сопоставление с несколькими шаблонами: Напишите функцию, которая принимает список и возвращает “Empty”, если список пуст, “Singleton”, если список содержит один элемент, и “Multiple”, если список содержит несколько элементов.
Сопоставление с кортежами из трёх элементов: Реализуйте функцию, которая принимает кортеж из трёх элементов и возвращает их сумму.

Лаб. работа №6 – Типы и классы типов

Цель работы

Закрепить создание пользовательских типов данных, работу с классами типов (type classes) и их экземплярами.

Самостоятельные задания:

Создание пользовательского типа данных: Создайте тип данных Color, который может представлять цвета: красный, зелёный, синий или их комбинацию (например, RGB).
Функция для работы с типом Color: Напишите функцию, которая принимает значение типа Color и возвращает его строковое представление.
Создание типа Point: Создайте тип данных Point, который представляет точку в двумерном пространстве (с координатами x и y).
Функция для вычисления расстояния между двумя точками: Напишите функцию, которая принимает два значения типа Point и возвращает расстояние между ними.
Создание типа Shape: Создайте тип данных Shape, который может представлять круг (Circle) или прямоугольник (Rectangle).
Функция для вычисления площади фигуры: Напишите функцию, которая принимает значение типа Shape и возвращает его площадь.
Создание класса типов Printable: Создайте класс типов Printable, который имеет один метод printMe, возвращающий строковое представление объекта.
Реализация экземпляров Printable: Сделайте тип Color экземпляром класса Printable.
Создание класса типов Area: Создайте класс типов Area, который имеет метод calculateArea, вычисляющий площадь объекта.
Реализация экземпляров Area: Сделайте тип Shape экземпляром класса Area.
Создание типа Maybe': Реализуйте свой аналог типа Maybe с именем Maybe', который может быть Just' или Nothing'.
Функция для работы с Maybe': Напишите функцию, которая принимает Maybe' Int и возвращает 0, если значение Nothing', иначе возвращает значение.
Создание класса типов Eq': Реализуйте свой аналог класса типов Eq с именем Eq', который имеет методы eq и notEq.
Реализация экземпляров Eq': Сделайте тип Color экземпляром класса Eq'.
Создание класса типов Ord': Реализуйте свой аналог класса типов Ord с именем Ord', который имеет методы compare', lessThan, greaterThan.
Реализация экземпляров Ord': Сделайте тип Point экземпляром класса Ord', сравнивая точки по расстоянию от начала координат.
Создание типа Tree: Реализуйте тип данных Tree, представляющий бинарное дерево.
Функция для обхода дерева: Напишите функцию, которая выполняет инфиксный обход дерева и возвращает список элементов.
Создание класса типов Functor': Реализуйте свой аналог класса типов Functor с именем Functor', который имеет метод map'.
Реализация экземпляров Functor': Сделайте тип Tree экземпляром класса Functor'.
Создание класса типов Monoid': Реализуйте свой аналог класса типов Monoid с именем Monoid', который имеет методы mempty' и mappend'.
Реализация экземпляров Monoid': Сделайте тип [a] (список) экземпляром класса Monoid'.
Создание класса типов Applicative': Реализуйте свой аналог класса типов Applicative с именем Applicative', который имеет методы pure' и apply'.
Реализация экземпляров Applicative': Сделайте тип Maybe' экземпляром класса Applicative'.
Создание класса типов Monad': Реализуйте свой аналог класса типов Monad с именем Monad', который имеет методы return' и bind'.
Реализация экземпляров Monad': Сделайте тип Maybe' экземпляром класса Monad'.

Лаб. работа №7 – Ленивые вычисления

Ленивые вычисления (lazy evaluation) — одна из ключевых особенностей Haskell, которая позволяет откладывать вычисления до тех пор, пока они действительно не понадобятся.

Цель работы

Закрепить использование ленивых вычислений.

Самостоятельные задания:

Бесконечный список чисел: Создайте бесконечный список натуральных чисел и извлеките из него первые 10 элементов.
Бесконечный список чётных чисел: Реализуйте бесконечный список чётных чисел и извлеките первые 5 элементов.
Бесконечный список чисел Фибоначчи: Создайте бесконечный список чисел Фибоначчи и извлеките первые 10 элементов.
Бесконечный список факториалов: Реализуйте бесконечный список факториалов и извлеките первые 5 элементов.
Бесконечный список степеней двойки: Создайте бесконечный список степеней двойки и извлеките первые 8 элементов.
Функция repeat: Реализуйте свою версию функции repeat, которая создаёт бесконечный список, состоящий из одного и того же элемента.
Функция cycle: Реализуйте свою версию функции cycle, которая бесконечно повторяет список.
Функция iterate: Реализуйте свою версию функции iterate, которая применяет функцию к начальному значению бесконечно.
Функция takeWhile: Реализуйте свою версию функции takeWhile, которая берёт элементы из списка, пока они удовлетворяют условию.
Функция dropWhile: Реализуйте свою версию функции dropWhile, которая удаляет элементы из начала списка, пока они удовлетворяют условию.
Бесконечный список простых чисел: Реализуйте бесконечный список простых чисел с использованием решета Эратосфена.
Бесконечный список треугольных чисел: Создайте бесконечный список треугольных чисел (чисел вида \(T_n = \frac{n(n+1)}{2}\)).
Бесконечный список квадратов: Реализуйте бесконечный список квадратов натуральных чисел.
Функция zipWith для бесконечных списков: Реализуйте свою версию функции zipWith, которая работает с бесконечными списками.
Функция interleave: Напишите функцию, которая чередует элементы двух бесконечных списков.
Бесконечный список чисел Фибоначчи с использованием zipWith: Реализуйте бесконечный список чисел Фибоначчи, используя функцию zipWith.
Бесконечный список чисел Фибоначчи с использованием scanl: Реализуйте бесконечный список чисел Фибоначчи, используя функцию scanl.
Функция unfoldr: Реализуйте свою версию функции unfoldr, которая генерирует список на основе функции и начального значения.
Бесконечный список чисел Фибоначчи с использованием unfoldr: Реализуйте бесконечный список чисел Фибоначчи, используя функцию unfoldr.
Функция map для бесконечных списков: Реализуйте свою версию функции map, которая работает с бесконечными списками.

Полезные ссылки

Наверх

Установка среды разработки для Haskell

Установка через GHCup

Установка через Chocolatey в привилегированном режиме

Установка через Chocolatey в непривилегированном режиме

Создать файл ChocolateyInstallNonAdmin.ps1 со следующим содержимым:

Открыть командную оболочку powershell.exe в том же каталоге, где сохранен скрипт из предыдущего пункта.

Выполнить в оболочке следующую команду:

Запустить .\ChocolateyInstallNonAdmin.ps1

Работа с Haskell в VSCode

Установка расширения

Создание файла исходного кода

Компиляция и запуск программы

Типы и функции в Haskell

Типы

Кортежи

Списки

Строки

Функции

Условные выражения

Функции многих переменных и порядок определения функций

Функции высшего порядка

Функция map

Функция filter

Функции foldr и foldl

Другие функции высшего порядка

Лямбда-абстракции

Секции

Лаб. работа №1 - Установка и настройка среды разработки

Лаб. работа №2 - Типы и функции

Цель работы

Самостоятельные задания:

Лаб. работа №3 – функции высших порядков

Цель работы

Самостоятельные задания:

Лаб. работа №4 – Рекурсия

Цель работы

Самостоятельные задания:

Лаб. работа №5 – Паттерн-матчинг

Цель работы

Самостоятельные задания:

Лаб. работа №6 – Типы и классы типов

Цель работы

Самостоятельные задания:

Лаб. работа №7 – Ленивые вычисления

Цель работы

Самостоятельные задания:

Полезные ссылки

Создать файл `ChocolateyInstallNonAdmin.ps1` со следующим содержимым:

Открыть командную оболочку `powershell.exe` в том же каталоге, где сохранен скрипт из предыдущего пункта.

Запустить `.\ChocolateyInstallNonAdmin.ps1`